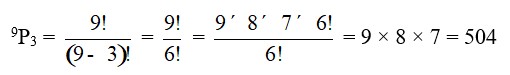Permutations and Combinations

19. Since no letter is repeated in the word EQUATION.

The permutation of 8 letters taken all at a time

= ⁸P₈

= $\frac{8!}{\left(8-8\right)!}$

= $\frac{8!}{0!}$

= 8! [since, 0! = 1]

= 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1

= 40320

16.The permutation of 8 persons taken 2 positions at a time is

15. The permutation of 5 different digits namely 1, 2, 3, 4, 5 taken 4 at a time is

⁵P₄ = $\frac{5!}{\left(5-4\right)!}$ = $\frac{5!}{1!}$ = 5 * 4 * 3 * 2 * 1 = 120

The permutation of having 2 or 4 at ones place is

²P₁ = $\frac{2!}{\left(2-1\right)!}$ = $\frac{2!}{1!}$ = 1 * 2 = 2

After fixing one of the even number at last digit we can rearrange the remaining four digits taking 3 at a time. i.e.

⁴P₃ = $\frac{4!}{\left(4-3\right)!}$ = $\frac{4!}{1!}$ = 4 * 3 * 2 * 1 = 24

Therefore, total permutation of 4 digit even number using 1, 2, 3, 4, 5

= 24 * 2

= 48

14. The permutation of having even number at the last digit from the given 6 different digits namely 1, 2, 3, 4, 5, 6 to form a 3-digit number is

After taking one of the even number as last digit we can rearrange the remaining 5 digits taking 2 at a time. i.e.

Therefore, The required number = 20 * 3 = 60

13. For every four-digit number we have to count the permutation of 10 digits namely 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 taken 4 at a time

However, these permutation will include those where 0 is at 1000's place.

So, fixing 0 at 1000's place and rearranging the remaining 9 digits taking 3 at a time.

Therefore, The required number = ¹⁰P₄ – ⁹P₃

= 5040 – 504

= 4536 ways

12. The permutation of 9 different digits taken 4 at a time is given by

11. i. n = 6, r = 2

$\frac{6!}{\left(6-2\right)!}$

= $\frac{6!}{4!}$

= $\frac{6*5*\left(4!\right)}{\left(4!\right)}$

= 30

ii. n = 9, r = 5

$\frac{9!}{\left(9-5\right)!}$

= $\frac{9!}{4!}$

= $\frac{9*8*7*6*5*\left(4!\right)}{4!}$

= 9 * 8 * 7 * 6 * 5

= 15,120

10. We have,

$\frac{1}{6!}$ + $\frac{1}{7!}$ = $\frac{x}{8!}$

=> $\frac{1}{6!}$ + $\frac{1}{7*6!}$ = $\frac{x}{8 *7*6!}$

=> 1 + $\frac{1}{7}$ = $\frac{x}{8*7}$

=> $\frac{8}{7}$ = $\frac{x}{8 *7}$

=>x = 8 * 8

=>x = 64

9.  $\frac{8!}{6! * 2!}$ = $\frac{8 *7*\left(6!\right) }{\left(6!\right)*1*2}$ = 4 * 7 = 28