Tags Physics Laws of Motion

Physics Laws of Motion

Get insights from 189 questions on Physics Laws of Motion, answered by students, alumni, and experts. You may also ask and answer any question you like about Physics Laws of Motion

Follow Ask Question

189

Questions

Discussions

Active Users

Followers

New answer posted

2 months ago

Physics Laws of Motion Class 11th

A football player is moving southward and suddenly turns eastward with the same speed to avoid an opponent. The force that acts on the player while turning is:

0 Follower 2 Views

Raj Pandey

Contributor-Level 9

Initial velocity $= - v \hat{j}$

Final velocity $= - v \hat{j}$

Change in velocity $= v \hat{i} - (- v \hat{j})$

$= v (\hat{i} + \hat{j})$ Momentum gain is along $\hat{i} + \hat{j}$

$\Rightarrow$ Force experienced is along $\hat{i} + \hat{j}$

$\Rightarrow$ Force experienced is in North-East direction.

0 0

New answer posted

2 months ago

Physics Laws of Motion Laws of Motion

Calculate the maximum acceleration of a moving car so that a body lying on the floor of the car remains stationary. The coefficient of static friction between the body and the floor is $0.15 (g = 10 {m s}^{- 2})$ .

0 Follower 8 Views

alok kumar singh

Contributor-Level 10

$R = R_{0} (1 + α Δ T)$

$\begin{array}{r} \Rightarrow 6.8 = 2 [1 + α * (80 - 0)] \\ \Rightarrow α = \frac{3.4 - 1}{80} \\ = 0.03 \\ = 3 * 10^{- 2}^{?} C^{- 1} \end{array}$

0 0

New answer posted

2 months ago

Physics Laws of Motion Class 11th

A football player is moving southward and suddenly turns eastward with the same speed to avoid an opponent. The force that acts on the player while turning is:

0 Follower 5 Views

alok kumar singh

Contributor-Level 10

$h_{max} = \frac{u^{2} {s i n}^{2} ? ?}{2 g} = \frac{280 * 280}{2 * 9.8} * \frac{1}{4}$

$= 1000 m$

0 0

New answer posted

2 months ago

Physics Laws of Motion Class 11th

A ball of mass 10kg, moving with a velocity 10√3 m/s along, the x-axis, hits another ball of mass 20kg which is at rest. After the collision, first ball comes to rest while second ball disintegrates into two equal pieces. One piece starts moving along y-axis with a speed of 10 m/s. The second piece starts moving at an angle of 30° with respect to the x-axis. The velocity of the ball moving at 30° with x-axis is x m/s. The configuration of pieces after collision is shown in the figure below. The value of x to the nearest integer is---------

0 Follower 8 Views

Raj Pandey

Contributor-Level 9

Apply conservation of momentum along y-axis, we can write
10v? - 10v? sin 30° = 0
⇒ v? = 20m/s

0 0

New answer posted

2 months ago

Physics Laws of Motion Class 11th

A boy of mass 4 kg is standing on a piece of wood having mass 5 kg. If the coefficient of friction between the wood and the floor is 0.5, the maximum force that boy can exert on the rope so that the piece of wood does not move from its place is _____ N. (Round off to the Nearest Integer) [Take g = 10 ms?²]

0 Follower 3 Views

alok kumar singh

Contributor-Level 10

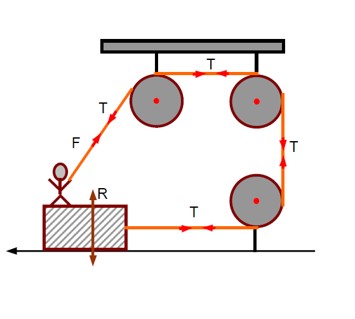
Assuming the rope in the boy's hand is vertical and using a Free Body Diagram (FBD):
f? = T
R + T = 90 ⇒ R = 90 - T
For the piece of wood not to move, f? ≤ µR:
T ≤ 0.5 (90 - T) ⇒ T ≤ 30N

0 0

New answer posted

2 months ago

Physics Laws of Motion Class 11th

A body of mass 1 kg rests on a horizontal floor with which it has a coefficient of static friction 1/√3. It is desired to make the body move by applying the minimum possible force F N. The value of F will be ______. (Round off to Nearest Integer) [Take g = 10 ms?²]

0 Follower 3 Views

alok kumar singh

Contributor-Level 10

The minimum force F? is calculated as:
F? = (μmg) / √* (1 + μ²)* = ( (1/√3) * 1 * 10 ) / √* (1 + (1/√3)²) = 5N

0 0

New answer posted

2 months ago

Physics Laws of Motion Class 11th

Two identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural L and spring constant K. A third block C of mass m moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is:

0 Follower 6 Views

alok kumar singh

Contributor-Level 10

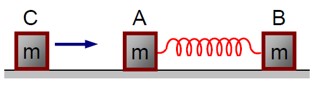
For an elastic collision where C comes to rest, and the compression in the spring is maximum, the velocities of A and B are equal (v). Using the conservation of mechanical energy:
(1/2)mv? ² = 2 * (1/2)mv² + (1/2)kx²
This gives the maximum compression x as:
x = v? * √* (m / 2k)*

0 0

New answer posted

2 months ago

Physics Laws of Motion Class 11th

Two blocks (m = 0.5kg and M = 4.5kg) are arranged on a horizontal frictionless table as shown in figure. The coefficient of static friction between the two blocks is 3/7. Then the maximum horizontal force that can be applied on the block so that blocks move together is ---------N. (Round off to the Nearest Integer) [ Take g as 9.8 ms^-2]

0 Follower 7 Views

Vishal Baghel

Contributor-Level 10

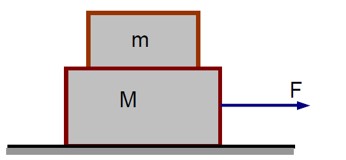
For the combined system of mass M and m, the acceleration under an applied force F is:
a = F / (M + m)

The static friction force (f_s) on the top block (m) provides its acceleration:
f_s = MA = m * [F / (M + m)] = mF / (M + m)

For the top block not to slip, the required static friction must be less than or equal to the maximum possible static friction (μmg):
f_s ≤ μmg
mF / (M + m) ≤ μmg
F ≤ μ (M + m)g

Using the values implied in the solution:
F ≤ 21 N

0 0

New answer posted

2 months ago

Physics Laws of Motion Class 11th

A modern grand - prix racing car of mass m is traveling on a flat track in a circular arc of radius R with a speed v. If the coefficient of static between the tyres and the track is µs, then the magnitude of negative lift F acting downwards on the car is : (Assume forces on the four tyres are identical and g = acceleration due to gravity)

0 Follower 3 Views

Vishal Baghel

Contributor-Level 10

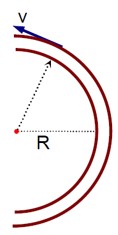
N = mg - F_L

f_s = mv²/R ≤ μsN = μs (mg - F_L)

F_L = m (v²/μsR - g)

0 0

New answer posted

2 months ago

Physics Laws of Motion Class 11th

A small ball of mass m is thrown upward with velocity u from the ground. The ball experiences a resistive force mkv² where v is it speed. The maximum height attained by the ball is:

0 Follower 16 Views

Vishal Baghel

Contributor-Level 10

Mg + MkV² = MA = -mv (dV/dx)
Vdv = (−) (g + kV²)dx
∫? (Vdv)/ (g + kv²) = ∫? - dx
[ln (g + kV²)/2k]? = -x
ln (g/ (g + ku²) = −2kx
x = (1/2k)ln (1 + ku²/g)

0 0

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
679k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Need guidance on career and education? Ask our experts

Your Question

Physics Laws of Motion

Questions

Discussions

Active Users

Followers

All

Discussions

Unanswered Questions

Share Your College Life Experience