Tags Physics Mechanical Properties of Fluids

Physics Mechanical Properties of Fluids

Get insights from 95 questions on Physics Mechanical Properties of Fluids, answered by students, alumni, and experts. You may also ask and answer any question you like about Physics Mechanical Properties of Fluids

Follow Ask Question

Questions

Discussions

Active Users

Followers

New answer posted

2 months ago

Physics Mechanical Properties of Fluids Class 11th

When a long glass capillary tube of radius 0.015 cm is dipped in a liquid, the liquid rises to a height of 15 cm within it. If the contact angle between the liquid and glass to close to 0°, the surface tension of the liquid, in milli Newton m?¹, is [ρ(liquid) = 900kgm?³, g = 10 ms?²] (Give answer in closest integer)

0 Follower 2 Views

alok kumar singh

Contributor-Level 10

The height of capillary rise is given by the formula:
h = (2T cosθ) / (rρg)
Given: h = 15 cm = 0.15 m, r = 0.015 cm = 1.5 * 10? m, ρ = 900 kg/m ³, g = 10 m/s², and θ ≈ 0° (so cosθ ≈ 1).
We need to find the surface tension, T.
T = (h r ρ g) / (2 cosθ)
T = (0.15 * 1.5 * 10? * 900 * 10) / 2
T = 0.10125 N/m
The answer is required in milliNewton m? ¹, so we multiply by 1000.
T = 101.25 mN/m.

0 0

New answer posted

2 months ago

Physics Mechanical Properties of Fluids Class 11th

Pressure inside two soap bubbles are 1.01 and 1.02 atmosphere, respectively. The ratio of their volumes is

0 Follower 5 Views

alok kumar singh

Contributor-Level 10

The excess pressure inside a soap bubble is given by ΔP = 4T/R, where T is the surface tension and R is the radius.
The pressures are given as P? = 1.01 atm and P? = 1.02 atm. Let the atmospheric pressure be P? = 1 atm.
ΔP? = P? - P? = 1.01 - 1 = 0.01 atm = 4T/R?
ΔP? = P? - P? = 1.02 - 1 = 0.02 atm = 4T/R?
Dividing the two equations: (ΔP? /ΔP? ) = (R? /R? )
0.01 / 0.02 = R? /R? ⇒ R? /R? = 2
The ratio of their volumes is V? /V? = ( (4/3)πR? ³ ) / ( (4/3)πR? ³ ) = (R? /R? )³ = 2³ = 8.
The ratio is 8:1.

0 0

New answer posted

2 months ago

Physics Mechanical Properties of Fluids Class 11th

A cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure. The radius of vessel is 5 cm and the angular speed of rotation is ω rads⁻¹. The difference in the height, h (in cm) of liquid at the centre of vessel and at the will be:

0 Follower 16 Views

alok kumar singh

Contributor-Level 10

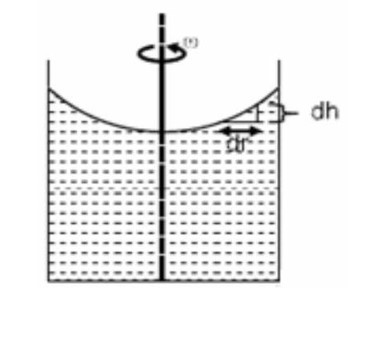
ρdrω²r = ρgdh
ω²∫? rdr = g∫? dh
ω²R²/2 = gh
h = ω²R²/2g = 25ω²/2g

0 0

New answer posted

2 months ago

Physics Mechanical Properties of Fluids Mechanical Properties of Fluids

In an experiment to verify Stokes law, a small spherical ball of radius r and density ρ falls under gravity through a distance h in air before entering a tank of water. If the terminal velocity of the ball inside water is same as its velocity just before entering the water surface, then the value of h is proportional to: (ignore viscosity of air)

0 Follower 3 Views

Vishal Baghel

Contributor-Level 10

√2gh = (2r²g/9η) (ρ_t - ρ)
⇒ h = (2/81) (r? g (ρ_t - ρ)²/η²)
⇒ h ∝ r?
After falling through h, the velocity be equal to terminal velocity.

0 0

New answer posted

2 months ago

Physics Mechanical Properties of Fluids Class 11th

A leak proof cylinder of length $1 m$ , made of a metal which has very low coefficient of expansion is floating vertically in water at $0^{?} C$ $^{}$ such that its height above the water surface is $20 c m$ . When the temperature of water is increased to $4^{?} C$ $^{}$ , the height of the cylinder above the water surface becomes $21 c m$ . The density of water at $T = 4^{?} C$ $^{}$ , relative to the density at $T = 0^{?} C$ $^{}$ is close to: