Physics NCERT Exemplar Solutions Class 11th Chapter Fifteen
Get insights from 80 questions on Physics NCERT Exemplar Solutions Class 11th Chapter Fifteen, answered by students, alumni, and experts. You may also ask and answer any question you like about Physics NCERT Exemplar Solutions Class 11th Chapter Fifteen
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
4 months agoContributor-Level 10
For no toppling
(in limiting case)
But is not possible as maximum value of ![]() can be equal to
can be equal to ![]() only.
only.
New answer posted
4 months agoContributor-Level 9
ε = |dΦ/dt| = A|dB/dt|
Given B (t), dB/dt = (4/π) * 10? ³ * (-1/100)
ε = (π * 1²) * | (4/π) * 10? ³ * (-1/100)|
= 4 * 10? V
To find when B=0:
B = 0 ⇒ 1 - t/100 = 0
⇒ t = 100 second
Energy Dissipated, E = P * t = (ε²/R) * t
E = (4*10? )² / (2*10? ) * 100 = 80mJ
New answer posted
4 months agoContributor-Level 9
We know, μ? = 1 + χ?
B? ∝ μ?
B ∝ μ
(ΔB/B? ) = (B-B? )/B? = (μ-μ? )/μ? = μ/μ? - 1 = μ? - 1 = χ?
% (ΔB/B) = χ? * 100 = 2.2 * 10? * 100 = 22/10?
(Note: The value for χ? in the source image appears to have a typo as 2.2 * 10? , it has been corrected to 2.2 * 10? to match the final answer.)
New answer posted
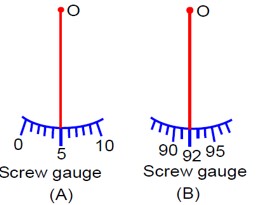
4 months agoContributor-Level 9
Difference in Reading = Positive Zero Error - Negative Zero Error
= (+5) - [- (100-92)]
= 5 - [-8]
= 13
New answer posted
4 months agoContributor-Level 9
Given: Power in R_B = 200 W, R_B = 50 Ω, V_source = 200 V
I² R_B = 200
I² (50) = 200
I² = 4 ⇒ I = 2A
Also, I = V_source / (R + R_B)
2 = 200 / (R + 50)
2 (R + 50) = 200
R + 50 = 100
R = 50Ω
New answer posted
4 months agoContributor-Level 9
From conservation of momentum:
2*4 = 2v? + mv?
Given v? = 1 m/s (interpreted from intermediate steps)
8 = 2 (1) + mv?
mv? = 6 . (i)
From coefficient of restitution (e=1 for elastic collision):
e = (v? - v? )/ (u? - u? )
1 = (v? - v? )/ (4 - 0)
-1 = (v? - v? )/ (0 - 4) (as written in the image)
⇒ 4 = v? - 1
⇒ v? = 5 . (ii)
Put (2) in (1), m (5) = 6
m = 1.2kg
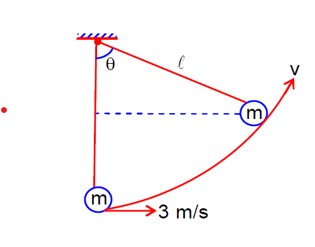
New answer posted
4 months agoContributor-Level 9
(1/2)mu² = (1/2)mv² + mgl (1-cosθ)
⇒ v² = u² - 2gl (1-cosθ)
⇒ v² = 3² - 2*10*0.5* (1 - 1/2)
⇒ v² = 9 - 5 = 4
v = 2m/s
New answer posted
4 months agoContributor-Level 9
I = I? e? /?
= (20/10000) e^- (1*10? / 10*10? ³)
= 2 * 10? ³ e? ¹
The provided solution calculates as:
= 2 * 10? ³ e? ¹
= 2e? ¹ mA
= 2 * 0.37mA
= 0.74 mA = 74/100 mA
(Note: There seems to be a calculation discrepancy in the source image, the steps shown lead to I = 2e? ¹ mA)
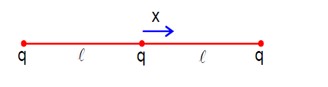
New answer posted
4 months agoContributor-Level 9
F_net = -kq²/ (l+x)² + kq²/ (l-x)²
= kq² [ (l+x)² - (l-x)² / (l²-x²)² ]
= kq² [ 4lx / (l²-x²)² ]
For x << l,
ma ≈ -4kq²x / l³
a = - (4kq²/ml³)x
ω² = 4kq²/ml³
ω = √ (4kq²/ml³)
= √ (4 * 9*10? * 10 / (1*10? * 1)
= 6 * 10? rad/s
= 6000 * 10? rad/s
New answer posted
4 months agoContributor-Level 9
ω = √k_eq/μ [μ = (m? )/ (m? +m? ) (Reduced mass)]
k_eq = (k * 4k)/ (k+4k) = 4k/5
ω = √ (4k/5) / (m? / (m? +m? )
= √ (4*20/5) / (0.2*0.8)/ (0.2+0.8)
= √ (16/0.16)
= 10 rad/s
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers