Physics NCERT Exemplar Solutions Class 11th Chapter Fourteen
Get insights from 42 questions on Physics NCERT Exemplar Solutions Class 11th Chapter Fourteen, answered by students, alumni, and experts. You may also ask and answer any question you like about Physics NCERT Exemplar Solutions Class 11th Chapter Fourteen
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
6 months agoContributor-Level 10
This is a multiple choice answer as classified in NCERT Exemplar
(a) Let angular velocity of the particle executing circular motion is w and when it is at O makes and angle
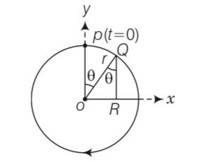
As =wt
OR=OQCos (90- )
= OQsin =OQsinwt
=rsinwt
x=rsinwt=Bsinwt
= Bsin =Bsin ( )
New answer posted
6 months agoContributor-Level 10
This is a multiple choice answer as classified in NCERT Exemplar
(b) A is given a transverse displacement. Through the elastic support the disturbance is transferred to all the pendulums.
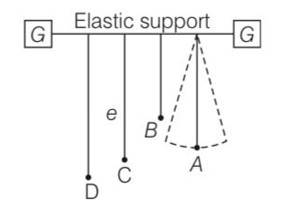
A and C are having same length hence they will be in resonance, because their time period of oscillation.
T= hence frequency is same. So amplitude of A and C will be maximum.New answer posted
6 months agoContributor-Level 10
This is a multiple choice answer as classified in NCERT Exemplar
(d) y= asinwt + bcoswt
a=Asin and b= Acos
a2+b2=A2sin2 +A2cos2
A=
y=Asin +Acos
= Asin (wt+ )
dy/dt= Awcos (wt+ )
So it is proportional to displacement . so follows SHM
New answer posted
6 months agoContributor-Level 10
This is a multiple choice answer as classified in NCERT Exemplar
(c) x= acoswt
Y= asinwt
Squaring and adding above eqns
x2+y2=a2, this is the equation of circle
New answer posted
6 months agoContributor-Level 10
This is a multiple choice answer as classified in NCERT Exemplar
(c) Consider the diagram in which a liquid column oscillates . in this case, restoring force acts on the liquid due to gravity.
Restoring force f = weight of liquid column of height 2y
t=-A = -2A
f
motion is SHM with force constant k= 2A
T= = 2
So time period is independent upon density of liquid.
New question posted
6 months agoNew answer posted
6 months agoContributor-Level 10
This is a multiple choice answer as classified in NCERT Exemplar
(d) For motion to be in SHM acceleration of the particle must be proportional to negative of displacement.

a , so y has to linear.
New answer posted
6 months agoContributor-Level 10
This is a multiple choice answer as classified in NCERT Exemplar
(b) y = sin3wt
= [3sinwt-4sin3wt]/4
dy/dt= [ ]/4
4dy/dt=3wcoswt-4 [3wcoswt]
4
= -
is not proportional to y. hence it is not SHM.
New answer posted
6 months agoContributor-Level 10
This is a multiple choice answer as classified in NCERT Exemplar
Velocity =dy/dt=
= 3 (-2w) [-sin ( )]
= 6wsin
Acceleration a = dv/dt=
= -4w2 [3cos ( )]
A = -4w2y hence acceleration is directly proportional to displacement so it follows SHM
w'= 2w
2
T'= 2 =
New answer posted
6 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
By considering the diagram
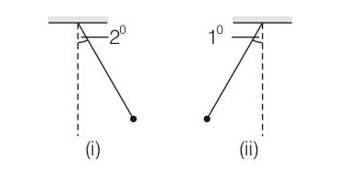
1=
2=
As it is clear given that amplitude time period being equal but phases being different. Now for first pendulum at any time t
1= 2
So sin = sin(wt+ )
wt+
where o=2o is the angular amplitude of first pendulum . for the second pendulum , the angular displacement is one degree , therefore 2= and negative sign is taken to show for being left to mean position.
-
Sin(wt+ )=-1/2
So (wt+ 2)=-
So by making their difference
(wt+ 2)-( 1)=7 =4
( 2- 1)= 1200
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers