Physics NCERT Exemplar Solutions Class 11th Chapter Fourteen
Get insights from 42 questions on Physics NCERT Exemplar Solutions Class 11th Chapter Fourteen, answered by students, alumni, and experts. You may also ask and answer any question you like about Physics NCERT Exemplar Solutions Class 11th Chapter Fourteen
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
6 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
Consider the diagram of the spring block system. It is a SHM with amplitude of 5cm about the mean position
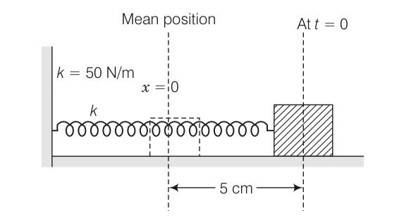
Spring constant k=50N/m
Mass =2kg
Angular frequency w=
Y (t)= Asin (wt+ )
Y (0)=Asin (w )
sin =1
y (t)=Asin (wt+ = Acoswt
A=5cm w=5rad/s
Y=5sin5t
New answer posted
6 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
given potential energy associated with the field
U (x)=Uo (1-cos )
F=-dU (x)/dx
F=-d (Uo-Uocos )=-Uo sin
F=-Uo
F
Motion is SHM for small oscillatons
F=-mw2X
Mw2=Uo
w2= , w=
T= =
New answer posted
6 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
Let us assume that the required displacement be x
Potential energy of the simple harmonic oscillator =1/2 kx2
k= force constant=mw2
PE= ½ mw2x2
Maximum energy of oscillator
TE= ½ mw2A2
PE=1/2 TE
½ mw2x2=
So x= =
New answer posted
6 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
As we know displacement y=sinwt-coswt
=
=
=
To comparing with standard equation
Y= asin (wt+ )
So T=2 /w
New answer posted
6 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
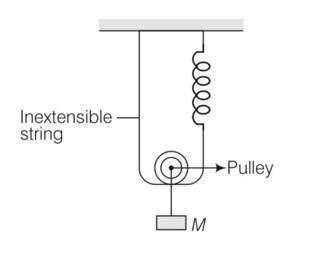
For calculation purpose, in this situation we will neglect gravity because it is constant throughout will not affect the net restoring force.
Let in the equilibrium position, the spring has extended by an amount xo
Let displacement by spring is and string be x .
But string is extensible so only spring will contribute in extension x+x=2x
So net extension is 2x+xo
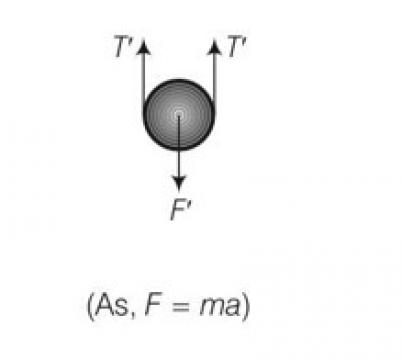
So force is F= 2T
T=kxo
F=2kxo
But when mass is lowered down further by x
F'=2T' but spring length is 2x+xo
F'=2k (2x+xo)
Restoring force on the system
Frestoring=- (F'-F)
So using above equations
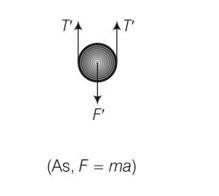
Frestoring= [2k (2x+x
New answer posted
6 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
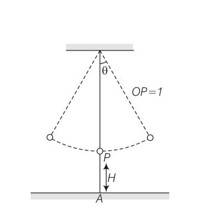
Let us assume t=0 when o then = 0coswt
Given a seconds pendulum w=2
=
At time t, let
Cos2 , t1=1/6
=-( )sin2
t=t1=1/6
d =- sin
the linear velocity is u=-
the vertical component is Uy=
the horizontal component Ux=-
at the time it snaps the vertical height is
H'=H+l(1-cos )
Let the time require for fall be t , then
H'= H+l (1 )
Let the time required for fall be at t then
H'=uyt+1/2 gt2
1/2gt2+
t=
given that is small , hence neglecting terms of order and higher
t=
H'
t=
the distance travelled in the x direction is uxt to the left of where
New answer posted
6 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
The gravitational force on the particle at a distance r from the centre of the earth arises entirely from that portion of matter of the earth in shells internal to the positiin of the particles . the external shells exert no force on the particle.
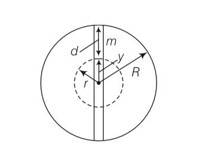
Let g' be the acceleration at P
So g' =g (1-d/R)=g (R-d/R)
R-d=y
g'=gy/R'
F=-mg'= -mgy/R
F
Ma=-Mgy/R, a = -gy/R
Comparing a=-w2y
w2=g/R
T=2
New answer posted
6 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
Let us consider an infinitesimal liquid column of length dx at a height x from horizontal line.
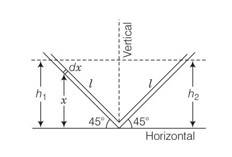
If density of the liquid
PE= dmgx=A
So total PE of the column
= =
But h1=lsin45
PE=A gl2sin245/2
Similarly PE of right column = A gl2sin245/2
Total PE = A gl2sin245/2+ A gl2sin245/2
= A gl2/2
If due to pressure difference is created y element of left side moves on the right side then liquid present in the left arm =l-y
But liquid present in the right arm =l+y
Total PE = PEfinal-PEinitial
Change in PE = ]
= =A
Change in KE = ½ mv2
m=A
change in KE= 1/2A =A
so from
New answer posted
6 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
Let the log be passed and the vertical displacement at the vertical displacement at the equilibrium position
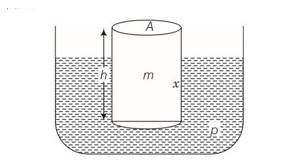
So mg= buoyant forces =
When it is displaced by further displacement x, the buoyant force is A (xo+x)
Net restoring force = buoyant forces -weight
=A (xo+x) -mg
=A
As displacement x is downward and restoring force is upward
Frestoring =-A =-kx
So motion is SHM
Acceleration a=Frestoring/m=-kx/m
a=-w2x
w2=k/m
w=
T= 2
New answer posted
6 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
(a) When the support of the hand is removed the body oscillates about mean position
Suppose x is the maximum extension in the spring when it reaches the lowest point in oscillation.
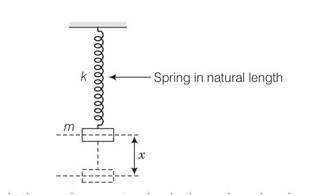
Loss in PE of the block=mgx
Gain in elastic potential energy =1/2 kx2
By energy conservation we cam say that
Mgx=1/2kx2
Or x= 2mg/k
Now the mean position of oscillation will be when the block is balanced by spring
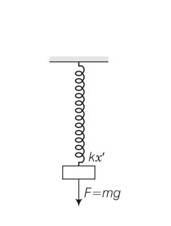
If x' is the extension in that case
F= kx'
F=mg
Mg=kx'
X'=mg/k
By dividing x by x'
x/x'=
so x=2x'
x'=4/2 =2cm
but the displacement of mass from the mean position when spring attains its natural l
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers