Physics NCERT Exemplar Solutions Class 12th Chapter Ten

This is a Long Answer Type Questions as classified in NCERT Exemplar

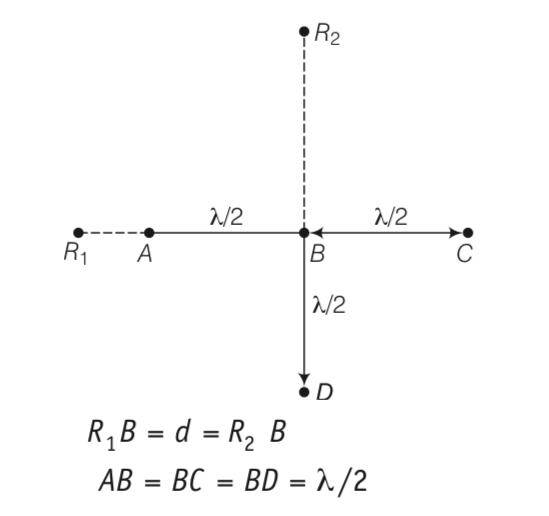
Explanation-consider the disturbance at the receiver R₁ which is at a distance d from B

Y_A= acos(wt)  and path difference is $\frac{\lambda }{2}$  hence phase difference is $\pi$ .

Thus the wave R₁ because of B

Y_B= acos(wt- $\pi$ )= - acoswt here path difference is $\lambda$  and hence phase difference is $2\pi$

Thus R₁ because of C

Y_c= acos(wt-2 $\pi$ )= acoswt

(i)let the signal picked up at R₂ from B be Y_B= a₁cos(wt)

The path difference between signal at D and that B is $\frac{\lambda }{2}$

Y_D= -a₁cos(wt)

The path difference between signal at A and that atB is

$\sqrt[]{d^2+{\left(\frac{\lambda }{2}\right)}^2}$ -d = d( ${1+\frac{{\lambda }^2}{4D^2})}^{1/2}$ -d = $\frac{{\lambda }^2}{8d^2}$

$asd?\lambda$  therefore path difference os 0

$phasedifference=\frac{2\pi }{\gamma }\frac{{\lambda }^2}{8d^2}$

_{$Y$ A}=a₁cos(wt- $\varnothing$ )

_{$Y$ C}=a₁cos(wt- $\varnothing$ )

Therefore signal picked up by R₂ is

Y_A+Y_b+Y_c+Y_d= y = 2a₁cos(wt- $\varnothing$ )

|y|² = 4a₁²cos²(wt- $\varnothing$ )

=2a₁². Thus R₁ picks up the larger signal.

(ii) if B is swiched off

R₁ picks up y = acoswt

^{IR1= $\frac{1}{2}$ a2}

R₂ picks up  y = a coswt

I_R2= $\frac{1}{2}$ a²

(iii) thus R₁ and R₂ pick up the same signal

If D is switched off

R₁ picks up by y = acoswt

I_R1= $\frac{1}{2}$ a²

Y= 3acoswt

I_R2=9a²/2

R₂ picks up larger signal compared to R₁

(iv) thus a signal at R₁ indicates B has been switched off and an enhanced signal at R₂ indicates D has been switched off.

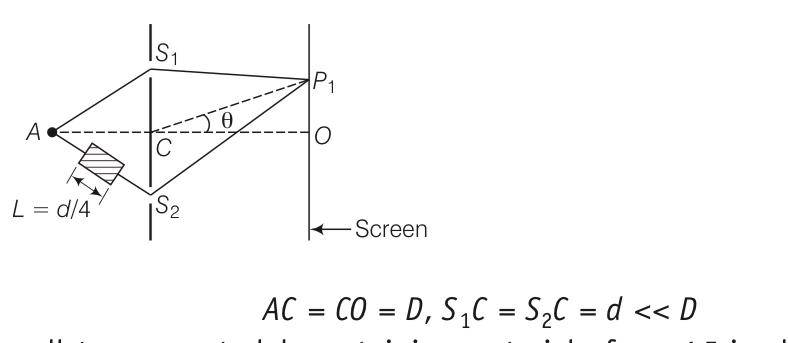
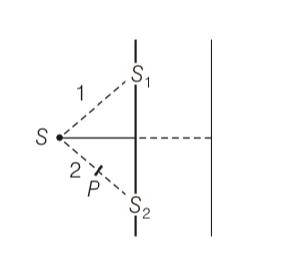
This is a Long Answer Type Questions as classified in NCERT Exemplar

Explanation- when polariser is not used

A=A_perp+A

letA₁= asinwt and A₂=asin(wt+ $\varnothing$ )

now superposition principle for perpendicular polariser

A_R= asinwt+ asin(wt+ $\varnothing$ )

A_R=a(2cos $\varnothing /2$ sin(wt+ $\varnothing$ ))

A_R=2acos $\varnothing /2$  sin(wt+ $\varnothing$ )

This eqn is also same for parallel polariser

A_R=2acos $\varnothing /2$  sin(wt+ $\varnothing$ )

And we know that intensity is directly proportional to square of amplitude

(A_R)²= (A_perp)²+(A)²

So resultant intensity is

I=4(a)²cos^{2 $\varnothing /2\frac{1}{T}{\int }_0^T{sin}^2(wt+\varnothing )$} dt + 4(a)²cos^{2 $\varnothing /2\frac{1}{T}{\int }_0^T{sin}^2(wt+\varnothing )$} dt

I= 8(a)²cos^{2 $\varnothing /2$} (1/2)                                     (after integrating sin value we got 1/2)

I= 4(a)²cos^{2 $\varnothing /2$}

So I= 4(a)²

But when there is a polariser

Perpendicular polariser is blocked

I=2(a)²cos^{2 $\varnothing /2\frac{1}{T}{\int }_0^T{sin}^2(wt+\varnothing )$} dt + (a)^{2 $\frac{1}{T}{\int }_0^T{sin}^2\left(wt\right)$}

I=2(a)²cos^{2 $\varnothing /2+$} 1/2(a)²

When $\varnothing =0$

I_max=2(a)²+1/2(a)²

I_max=5/2(a)²

I_max=5/2(I/4)=5I/8

At first minima it becomes I/8