Physics NCERT Exemplar Solutions Class 11 Chapter Two is titled Units and Measurements. It is an important chapter for the Class 11 examination and also for future studies of Physics. To have a strong foundation and understanding of the concepts related to this chapter, one needs to study it thoroughly.
Students can refer to Shiksha's NCERT Solutions for Class 11 Physics Chapter 2 Units and Measurements for better understanding. It is created by the subject matter experts and offers reliable study material.
In the Class 11th Chapter One Units and Measurements Exemplar, the student will also get the Physics NCERT Exemplar Class 11 PDF. The students can download this PDF for study at their own schedule. It contains all the questions of the NCERT Exemplar book. The PDF also includes sample papers and question papers from previous years.
Chapter 2 covers the International System of Units (SI Units), measurements of Mass, length, time, significant figures, precision, accuracy, errors in measurement, applications, and limitations of dimensional analysis. It also includes the dimensions of physical quantities, dimensional formulae, and equations. One can find the NCERT solutions for all Physics Chapters on Shiksha.
- NCERT Exemplar 11 Units and Measurements PDF
- Units and Dimensions Questions and Answers
- Common Mistakes and Tips for NCERT Physics Exemplar Chapter 2
- Important Formulas Related to Physics Chapter 1 NCERT Exemplar
- JEE Mains 2022
NCERT Exemplar 11 Units and Measurements PDF
The students can download the NCERT Exemplar Solutions for Class 11 Physics Chapter 2 – Units and Measurement PDF from here. It is created by the Shiksha experts and is according to the latest NCERT and CBSE updates. This provides an effective tool to revise the entire unit and measurement syllabus, as it covers all exercise questions from Chapter 2.
Students looking to read from the NCERT notes for quick revision can read them at NCERT Notes for Class 11 & 12.
Units and Dimensions Questions and Answers
| 2.1 A new system of units is proposed in which unit of mass is α kg, unit of length β m and unit of time γ s. How much will 5 J measure in this new system? |
| Explanation- Energy E= [ML2T-2] Let M1,L1and T1 and M2,L2and T2 are fundamental quantities for two units M1=1kg and L1=1m and T1=1s M2= αkg, L2= β m and T2= γ s And n1u1=n2u2 |
| 2.2 The volume of a liquid flowing out per second of a pipe of length l and radius r is written by a student as V= where P is the pressure difference between the two ends of the pipe and η is coefficent of viscosity of the liquid having dimensional formula ML-1 T-1. Check whether the equation is dimensionally correct. |
| Explanation- Rate of flow is equal to V= Dimensions of V or LHS= volume/time=L3/T=[L3T-1] Dimensions of P= [ML-1T-2] Dimensions of =[ML-1T-1] Dimensions of L= [L] Dimensions of r=[L] Dimensions of RHS= So they are in equal in dimensions. So equation is correct dimensionally. |
| 2.3 A physical quantity X is related to four measurable quantities a, b, c and d as follows: X = a2 b3 c5/2 d-2 The percentage error in the measurement of a, b, c and d are 1%, 2%, 3% and 4%, respectively. What is the percentage error in quantity X ? If the value of X calculated on the basis of the above relation is 2.763, to what value should you round off the result. |
| Explanation- As we know that X= a2 b3 c5/2 d-2 Maximum percentage error in X is =
Mean absolute error in X= rounding off to significant value. And calculated value would be 2.8 rounding off upto two digits. |
| 2.4 In the expression P = E l2m-5 G-2, E, m, l and G denote energy, mass, angular momentum and gravitational constant, respectively. Show that P is a dimensionless quantity. |
| Explanation- Dimensions of energy is E=[ML2T-2] Mass m=[M] Dimension of E= [ML2T-2] Dimensions of L= [ML-2T-1] Dimensions of G= [M-1L3T-2] By using these values [P]=[ML2T-2] 2 -2 =[M1+2-5+2L2+4-6T-2-2+4] =[M0L0T0] After we know that P is dimensionless quantity |
Commonly asked questions
(a) How many astronomical units (A.U.) make 1 parsec?
(b) Consider a sunlike star at a distance of 2 parsecs. When it is seen through a telescope with 100 magnification, what should be the angular size of the star? Sun appears too be (1/2)° from the earth. Due to atmospheric fluctuations, eye can’t resolve objects smaller than 1 arc minute.
(c) Mars has approximately half of the earth’s diameter. When it is closest to the earth it is at about 1/2 A.U. from the earth. Calculate what size it will appear when seen through the same telescope.
This is a long answer type question as classified in NCERT Exemplar
(a) 1 parsec =distance at which 1AU long arc subtends an angle of 1sec
1parsec = ( )
1 deg = 3600 arc sec
1 parsec =
1parsec = = 2
(b) sun’s diameter is 1/20
so at 1 parsec star is degree in diameter= 15 10-5 arc/min with magnification it looks like 15 10-3
(c)
we know that
At 1AU sun’s diameter =1/20
Mars diameter =
AT 1/2AU
Mars diameter will 1/2000 but with hundred magnification it is 1/20
Einstein’s mass - energy relation emerging out of his famous theory of relativity relates mass (m ) to energy (E ) as E = mc2, where c is speed of light in vacuum. At the nuclear level, the magnitudes of energy are very small. The energy at nuclear level is usually measured in MeV, where 1 MeV= 1.6×10-13 J; the masses are measured in unified atomic mass unit (u) where 1u = 1.67 × 10-27 kg.
(a) Show that the energy equivalent of 1 u is 931.5 MeV.
(b) A student writes the relation as 1 u = 931.5 MeV. The teacher points out that the relation is dimensionally incorrect. Write the correct relation.
This is a long answer type question as classified in NCERT Exemplar
(a) 1 amu = 1.67 10-27kg
And energy E=mc2= (1.67 10-27) (3 )2J
E= 939.4MeV
(b) So dimensionally correct relation will be E=amu c2
= 1uc2
= 931.5MeV
An artificial satellite is revolving around a planet of mass M and radius R, in a circular orbit of radius r. From Kepler’s Third law about the period of a satellite around a common central body, square of the period of revolution T is proportional to the cube of the radius of the orbit r. Show using dimensional analysis, that
T= ,
where k is a dimensionless constant and g is acceleration due to gravity.
This is a long answer type question as classified in NCERT Exemplar
According to kepler’s law T2 r3
T
T
T
[M0L0T]=K [L]3/2 [L]a [LT-2]b
= k [La+b+3/2T-2b]
On comparing the powers of same terms we get
So a+b+3/2=0
So b=-1/2 and a=-1
T=kr3/2R-1g-1/2
T=
In the expression P = E l2m-5 G-2, E, m, l and G denote energy, mass, angular momentum and gravitational constant, respectively. Show that P is a dimensionless quantity.
This is a long answer type question as classified in NCERT Exemplar
Dimensions of energy is E= [ML2T-2]
Mass m= [M]
Dimension of E= [ML2T-2]
Dimensions of L= [ML-2T-1]
Dimensions of G= [M-1L3T-2]
By using these values [P]= [ML2T-2] 2 -2
= [M1+2-5+2L2+4-6T-2-2+4]
= [M0L0T0]
After we know that P is dimensionless quantity
In an experiment to estimate the size of a molecule of oleic acid 1 mL of oleic acid is dissolved in 19 mL of alcohol. Then 1 mL of this solution is diluted to 20 mL by adding alcohol. Now 1 drop of this diluted solution is placed on water in a shallow trough. The solution spreads over the surface of water forming one molecule thick layer. Now, lycopodium powder is sprinkled evenly over the film and its diameter is measured. Knowing the volume of the drop and area of the film we can calculate the thickness of the film which will give us the size of oleic acid molecule. Read the passage carefully and answer the following questions:
(a) Why do we dissolve oleic acid in alcohol?
(b) What is the role of lycopodium powder?
(c) What would be the volume of oleic acid in each mL of solution prepared?
(d) How will you calculate the volume of n drops of this solution of oleic acid?
(e) What will be the volume of oleic acid in one drop of this solution?
This is a long answer type question as classified in NCERT Exemplar
(a) Oleic acid does not dissolve in water hence, it is dissolved in alcohol.
(b) Lycopodium powder spreads over the entire surface of water when it is sprinkled evenly. When a drop of prepared solution is dropped on water, oleic acid does not dissolve in water. Instead it spreads on the water surface pushing the lycopodium powder away to clear a circular area where the drop falls.
(c) In each mL of solution volume of oleic acid = 1/20mL = 1/400mL
(d) Volume of n drops of this solution of oleic acid can be calculated by burette and measuring cylinder
(e) If n drops of sodium solution make 1mL, the volume of oleic acid in one drop will be mL
Why do we have different units for the same physical quantity?
This is a short answer type question as classified in NCERT Exemplar
The value of any given physical quantity may very over a wide range. Therefore different units of same physical quantity are required. As we know that to measuring distance of an object we need cm m, km, light year etc.
The distance of a galaxy is of the order of 1025 m. Calculate the order of magnitude of time taken by light to reach us from the galaxy.
This is a short answer type question as classified in NCERT Exemplar
Distance of galaxy = 1025m
Speed of light = 3 108 m/s
T = distance /speed =
s
Time for 20 oscillations of a pendulum is measured as t1= 39.6 s; t 2= 39.9 s; t 3= 39.5 s. What is the precision in the measurements? What is the accuracy of the measurement?
This is a short answer type question as classified in NCERT Exemplar
t1=39.6s, t2=39.9s and t3=39.5s
Least count of measuring instrument =0.1s
Precision in the measurement =least count of the measuring instrument =0.1s
So mean value of 20 observation
Mean value of t=
Absolute error in
t1= t-t1 = 39.7-39.6 =0.1s
In t2= t-t2 = 39.7-39.9=-0.2s
In t3= t-t1 = 39.7-39.5= 0.2s
Mean error =
Accuracy in the measurement =
The sum of the numbers 436.32, 227.2 and 0.301 in appropriate significant figures is
(a) 663.821
(b) 664
(c) 663.8
(d) 663.82
This is a multiple choice answer as classified in NCERT Exemplar
(b) The sum of these numbers is 663.821. The number with least decimal places is 227.2 is correct to only one decimal places and the closest number to it 664.
A new system of units is proposed in which unit of mass is α kg, unit of length β m and unit of time γ s. How much will 5 J measure in this new system?
This is a long answer type question as classified in NCERT Exemplar
Energy E= [ML2T-2]
Let M1, L1 and T1 and M2, L2 and T2 are fundamental quantities for two units
M1=1kg and L1=1m and T1=1s
M2= α kg, L2= β m and T2= γ s
And n1u1=n2u2
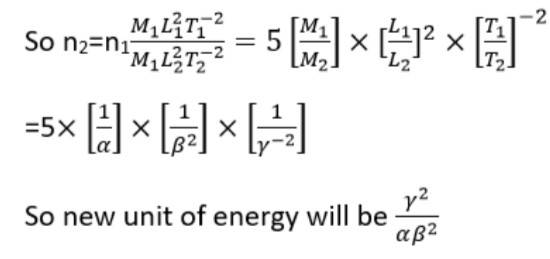
The volume of a liquid flowing out per second of a pipe of length l and radius r is written by a student as
V=
where P is the pressure difference between the two ends of the pipe and η is coefficent of viscosity of the liquid having dimensional formula ML-1 T-1. Check whether the equation is dimensionally correct.
This is a long answer type question as classified in NCERT Exemplar
Rate of flow is equal to V=
Dimensions of V or LHS= volume/time=L3/T= [L3T-1]
Dimensions of P= [ML-1T-2]
Dimensions of = [ML-1T-1]
Dimensions of L= [L]
Dimensions of r= [L]
Dimensions of RHS=
So they are in equal in dimensions.
So equation is correct dimensionally.
A physical quantity X is related to four measurable quantities a, b, c and d as follows:
X = a2 b3 c5/2 d-2
The percentage error in the measurement of a, b, c and d are 1%, 2%, 3% and 4%, respectively. What is the percentage error in quantity X ? If the value of X calculated on the basis of the above relation is 2.763, to what value should you round off the result.
This is a long answer type question as classified in NCERT Exemplar
As we know that X= a2 b3 c5/2 d-2
Maximum percentage error in X is
=
Mean absolute error in X= rounding off to significant value.
And calculated value would be 2.8 rounding off upto two digits.
If velocity of light c, Planck’s constant h and gravitational constant G are taken as fundamental quantities then express mass, length and time in terms of dimensions of these quantities.
This is a long answer type question as classified in NCERT Exemplar
(i) dimension of h = [ML2T-1]
And c= [LT-1] and dimension of G= [M-1L3T-2]
Let m= kcxhyGz
[ML0T0]= [LT-1]x [ML2T-1]y [M-1L3T-2]z
= [My-zLx+2y+3zT-x-y-2z]
y-z=1
x+2y+3z=0
-x-y-2z=0
On solving these equation we got x= ½ y= ½ and z= -½
So formula will coming out from this is m=k
(ii) L=kcxhyGz
ao [M0LT0]= [LT-1]x [ML2T-1]y [M-1L3T-2]z
= [My-zLx+2y+3zT-x-y-2z]
y-z=0
x+2y+3z=1
-x-y-2z=0
After solving we get x= -3/2 y=1/2 and z=1/2
We got the formula is L=k
(iii)T= kcxhyGz
[M0L0T]= [LT-1]x [ML2T-1]y [M-1L3T-2]z
= [My-zLx+2y+3zT-x-y-2z]
On comparing powers we got x= -5/2 y=1/2 and z= ½
So formula for this would be T= k
The radius of atom is of the order of 1 Å and radius of nucleus is of the order of fermi. How many magnitudes higher is the volume of atom as compared to the volume of nucleus?
This is a short answer type question as classified in NCERT Exemplar
Radius of atom = 1Ao=10-10m
Radius of nucleus = 10-15m
Volume of atom=VA= 4/3 r3a
Volume of nucleus VN=4/3 r3N
To finding the ratio
Name the device used for measuring the mass of atoms and molecules.
This is a short answer type question as classified in NCERT Exemplar
A mass spectrograph is used for measuring the mass of atoms and molecules.
Express unified atomic mass unit in kg.
This is a short answer type question as classified in NCERT Exemplar
One atomic mass unit is 1/12 of the mass of carbon atom
Mass of one carbon atom = 12g
Number of atoms in one mole= Avogadro’s number
= 6.023 1023
Mass of one 6C12 atom =
1 amu= 1/12 of mass of carbon atom
1 amu= ( )g= 1.67
A function f (θ ) is defined as: 1- Why is it necessary for q to be a dimensionless quantity?
This is a short answer type question as classified in NCERT Exemplar
Since f ( is a sum of different powers of an we know that it is a dimensionless quantity. By principle of homogeneity as RHS is dimensionless. Hence LHS should also be dimensionless.
Why length, mass and time are chosen as base quantities in mechanics?
This is a short answer type question as classified in NCERT Exemplarv
Because they cannot be derived from one another as they are independent quantities.
Also we can say that all other quantities in mechanics can be expressed in terms of length mass and time.
(a) The earth-moon distance is about 60 earth radius. What will be the diameter of the earth (approximately in degrees) as seen from the moon?
(b) Moon is seen to be of (½)° diameter from the earth. What must be the relative size compared to the earth?
(c) From parallax measurement, the sun is found to be at a distance of about 400 times the earth-moon distance. Estimate the ratio of sun-earth diameters.
This is a short answer type question as classified in NCERT Exemplar
(a)
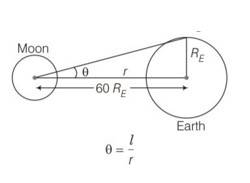
l=RE; r= 60RE
Hence angle subtend is
(b) But in 2nd case it is given that moon is (½)° and earth is 2o so it become 4 times.
(c) To measure parallax sun is about 400 times the earth moon distance hence
To finding ratio of
so
so
Which of the following time measuring devices is most precise?
(a) A wall clock.
(b) A stop watch.
(c) A digital watch.
(d) An atomic clock.
Give reason for your answer.
This is a short answer type question as classified in NCERT Exemplar
(a) A wall clock can measure time correctly upto one second .
(b) A stop watch can measure time correctly upto a fraction of a second .
(c) A digital watch upto the same precision
(d) An atomic clock measure more accurately.
The vernier scale of a travelling microscope has 50 divisions which coincide with 49 main scale divisions. If each main scale division is 0.5 mm, calculate the minimum inaccuracy in the measurement of distance.
This is a short answer type question as classified in NCERT Exemplar
It is given that 50 VSD
1MSD = 50/49VSD
1VSD= 49/50MSD
Minimum inaccuracy = 1MSD-1VSD= 1MSD-49/50MSD=1/50 MSD
1MSD= 0.5mm
Minimum inaccuracy = 1/50 0.5mm=0.01mm
During a total solar eclipse the moon almost entirely covers the sphere of the sun. Write the relation between the distances and sizes of the sun and moon.
This is a short answer type question as classified in NCERT Exemplar
Rme= distance of moon from earth
Rse=distance of sun from earth
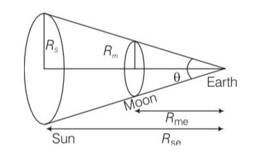
Let angle made by sun and moon is .
( )2 = ( )2
( )= ( )
Hence radius of sun and moon represents their sizes respectively.
If the unit of force is 100 N, unit of length is 10 m and unit of time is 100 s, what is the unit of mass in this system of units?
This is a short answer type question as classified in NCERT Exemplar
F= [MLT-2]=100N…….1
Length L= 10m………….2
Time t= 100s……….3
Substituting the value of L and T in eqn 1,2,3
M
M=100
M= 105kg
Give an example of
(a) A physical quantity which has a unit but no dimensions.
(b) A physical quantity which has neither unit nor dimensions.
(c) A constant which has a unit.
(d) A constant which has no unit.
This is a short answer type question as classified in NCERT Exemplar
(a) Plane angle = l/r radian its si unit is radian but no dimension formula.
(b) Strain= so no dimension
And g =9.8m/s2
(c) Gravitational constant G= 6.67
(d) Reynold’s number is a number having no dimension.
Calculate the length of the arc of a circle of radius 31.0 cm which subtends an angle of 6 π at the centre.
This is a short answer type question as classified in NCERT Exemplar
As we know,
L=31
Rounding off to three significant figures it would be 16.2cm
Calculate the solid angle subtended by the periphery of an area of 1cm2 at a point situated symmetrically at a distance of 5 cm from the area.
This is a short answer type question as classified in NCERT Exemplar
The formula for solid angle is
solid angle = area/ (distance)2
=
The displacement of a progressive wave is represented by y = A sin(wt – k x ), where x is distance and t is time. Write the dimensional formula of (i) ω and (ii) k.
This is a short answer type question as classified in NCERT Exemplar
For dimensional consistency LHS = RHS
[L]= [A]=L
As wt-kx should be dimensionless [wt]= [kx]=1
w [T]=k [L]=1
So w= [T]-1 and k= [L]-1
The number of significant figures in 0.06900 is
(a) 5
(b) 4
(c) 2
(d) 3
This is a multiple choice answer as classified in NCERT Exemplar
(b) The zero after points are not significant. The number can be written as 0.069, Hence number of significant figure are four.
The mass and volume of a body are 4.237 g and 2.5 cm3, respectively. The density of the material of the body in correct significant figures is
(a) 1.6048 g/cm3
(b) 1.69 g/cm3
(c) 1.7 g/cm3
(d) 1.695 g/cm3
This is a multiple choice answer as classified in NCERT Exemplar
(c) As we know that formula for density is
density = so density is 1.7g/cm3
The numbers 2.745 and 2.735 on rounding off to 3 significant figures will give
(a) 2.75 and 2.74
(b) 2.74 and 2.73
(c) 2.75 and 2.73
(d) 2.74 and 2.74
This is a multiple choice answer as classified in NCERT Exemplar
(d) Rounding off 2.745 to 3 significant figures would be 2.74 so result after in three significant figures is 2.74.
The length and breadth of a rectangular sheet are 16.2 cm and 10.1cm, respectively. The area of the sheet in appropriate significant figures and error is
(a) 164 ± 3 cm2
(b) 163.62 ± 2.6 cm2
(c) 163.6 ± 2.6 cm2
(d) 163.62 ± 3 cm2
This is a multiple choice answer as classified in NCERT Exemplar
(a) Given length = (1.62 )cm
And breadth b= (10.1 )cm
Area = l b=163.62 cm2
But when we rounding off to three significant figures then it would be =164cm2
= 2.63cm2
So by rounding it off it become 3cm2
Area A= (164 )cm2
Which of the following pairs of physical quantities does not have same dimensional formula?
(a) Work and torque.
(b) Angular momentum and Planck’s constant.
(c) Tension and surface tension.
(d) Impulse and linear momentum.
This is a multiple choice answer as classified in NCERT Exemplar
(c) (a) work =force [MLT-2] [L]= [ML2T-2]
Torque= force (distance)= [ML2T-2]
(b) angular momentum = mvr = [MLT-1] [L]= [ML2T-1]
Planck’s constant= E/V= [ML2T-2]/ [T-1]= [ML2T-1]
(c) tension=force= [MLT-2]
Surface tension = force/length= [MLT-2]/L= [ML0T-2]
(d) impulse =force (time)= [MLT-2] [T]= [MLT-1]
linear momentum = mass (velocity)= [M] [LT-1]
They both have different formula.
Measure of two quantities along with the precision of respective measuring instrument is
A = 2.5 m s–1 ± 0.5 m s-1
B = 0.10 s ± 0.01 s .
The value of A B will be
(a) (0.25 ± 0.08) m
(b) (0.25 ± 0.5) m
(c) (0.25 ± 0.05) m
(d) (0.25 ± 0.135) m
This is a multiple choice answer as classified in NCERT Exemplar
(a) As it is given that
A=2.5ms-1 0.5ms-1,
B= 0.10s 0.01s
X= AB= (2.5) (0.10)=0.25m
After rounding off two significant figures
AB= (0.25 )m
You measure two quantities as A = 1.0 m ± 0.2 m, B = 2.0 m ± 0.2 m. We should report correct value for as:
(a) 1.4 m ± 0.4 m
(b) 1.41m ± 0.15 m
(c) 1.4m ± 0.3 m
(d) 1.4m ± 0.2 m
This is a multiple choice answer as classified in NCERT Exemplar
(d) According to question
A= 1.0m 0.2m, B= 2 m
Y=
After rounding off 1.4m
=
=
After rounding off it becomes 0.2m
Thus the correct value of =r+dr
so its value become 1.4 0.2m
Which of the following measurements is most precise?
(a) 5.00 mm
(b) 5.00 cm
(c) 5.00 m
(d) 5.00 km
This is a multiple choice answer as classified in NCERT Exemplar
(a) All the given value are correct upto two decimal places. Here 5.00mm has the smallest unit and the error in 5.00mm is least so the smallest value has less error so 5.00mm is the most precise value.
The mean length of an object is 5 cm. Which of the following measurements is most accurate?
(a) 4.9 cm
(b) 4.805 cm
(c) 5.25 cm
(d) 5.4 cm
This is a multiple choice answer as classified in NCERT Exemplar
(a) l = 5cm
So by checking it
l1 = 5-4.9 = 0.1cm
l2= 5-4.805 = 0.195cm
l3= 5.25-5 = 0.25cm
l4= 5.4-5 = 0.4cm
now = 5-4.9= 01cm
has the least error hence 4.9 is the most precise value.
Young’s modulus of steel is 1.9 × 1011 N/m2. When expressed in CGS units of dynes/cm2, it will be equal to (1N = 105 dyne, 1m2 = 104 cm2)
(a) 1.9 × 1010
(b) 1.9 × 1011
(c) 1.9 × 1012
(d) 1.9 × 1013
This is a multiple choice answer as classified in NCERT Exemplar
(c) Y= 1.9×1011N/m2
1N=105dyne
Y= 1.9×1011×105dyne/1002cm2
1m= 100 cm
Y= 1.9
Y= 1.9
Y= 1.9 1012dyne/cm2
If momentum (P ), area (A) and time (T ) are taken to be fundamental quantities, then energy has the dimensional formula
(a) (A-1 T1)
(b) (A T)
(c) ( A-1/2 T)
(d) ( A1/2 T-1)
This is a multiple choice answer as classified in NCERT Exemplar
(d) E=
E=
E= [ML2T-2] and
A= [L2] and T= [T]
E= [k] [ ]a [A]b [T]c
ML2T-2= [MLT-1]a [L2]b [T]c
= MaL2b+aT-a+c
by principle of homogeneity we get,
ML2T-2= MaL2b+aT-a+c
After solving
A=1, 2b+a=2
So 2b+1=2
2b=1, b= ½
C=-2+a, c=-2+1, c=-1
So formula become
E= A1/2T-1
On the basis of dimensions, decide which of the following relations for the displacement of a particle undergoing simple harmonic motion is not correct:
(a) y = a sin 2πt/ T
(b) y =a sin v t.
(c) y = sin( )
(d) y =a (sin )
This is a multiple choice answer as classified in NCERT Exemplar
(b, c) for (c) LHS = [L]
RHS= [L/T]=LT-1
LHS RHS
Hence is c option is not correct.
In option (b) dimension of angle is vt i.e =L
RHS= L.L=L2 and LHS = L
LHS RHS
So option b is also not correct
LHS and RHS in both equation B and C are not equal.
If P, Q, R are physical quantities, having different dimensions, which of the following combinations can never be a meaningful quantity?
(a) (P – Q)/R
(b) PQ – R
(c) PQ/R
(d) (PR – Q2)/R
(e) (R + Q)/P
This is a multiple choice answer as classified in NCERT Exemplar
(a, e) It is given that P, Q, R are having different dimensions. Hence cannot be added or subtracted, so we can say that (a) and (e) are not meaningful. We cannot say about the dimensions of product of these quantities. Hence b, c and d may be meaningful.
Photon is quantum of radiation with energy E = hν where ν is frequency and h is Planck’s constant. The dimensions of h are the same as that of
(a) Linear impulse
(b) Angular impulse
(c) Linear momentum
(d) Angular momentum
This is a multiple choice answer as classified in NCERT Exemplar
(b, d) as we know E= hv
So h=E/v= =ML2T-1
Dimension of linear impulse = dimensions of momentum= [MLT-1]
As we know that J=
Angular impulse =tdt= = change in angular momentum
Hence angular momentum is [ML2T-1] same as the dimension of h.
If Planck’s constant (h ) and speed of light in vacuum (c ) are taken as two fundamental quantities, which one of the following can, in addition, be taken to express length, mass and time in terms of the three chosen fundamental quantities?
(a) Mass of electron (me )
(b) Universal gravitational constant (G )
(c) Charge of electron
(d) Mass of proton (mp)
This is a multiple choice answer as classified in NCERT Exemplar
(a,b,d) h=[ML2T-1]
[c]=[LT-1], [me]=M
[G]= [M-1L3T-2]
[e]=[AT],[mp]=[M]
[ ] =
M=
L=
C= LT-1
T= =
Hence a,b and d any can be used to express L,M and T in terms of three chosen fundamental quantities.
Which of the following ratios express pressure?
(a) Force/Area
(b) Energy/Volume
(c) Energy/Area
(d) Force/Volume
This is a multiple choice answer as classified in NCERT Exemplar
(a, b) we know that pressure = force/area
Pressure=
So we can say that pressure is also equal to energy per unit volume.
Which of the following are not a unit of time?
(a) Second
(b) Parsec
(c) Year
(d) Light year
This is a multiple choice answer as classified in NCERT Exemplar
(b, d) We know that one light year = 9.46 = distance that light travels in 1 year with a speed 3 m/s
1 par sec =3.08 = distance at which average radius of earth’s orbit subtends an angle of par second.
Here second and year represent time.
Common Mistakes and Tips for NCERT Physics Exemplar Chapter 2
Following are the common mistakes in units and measurements class 11:
- Mixing up base units with derived units. To avoid these mistakes, students can memorize the 7 SI base quantities and understand how combinations of these create derived units.
- Another common mistake is incorrectly writing dimensions and solutions. To avoid these, they can use dimensional formulas.
- Inconsistently applying rules for significant figures in addition/subtraction or multiple/division. Keep more significant figures with the least significant figures.
- Not analyzing types of errors and converting quantities without adjusting for powers correctly.
Some common tips to avoid these mistakes:
Instead of memorizing, try to understand the topics and formulas. The focus should be more on conceptual clarity rather than writing note formulas.
Familiarize yourself with parsec, light year, and astronomical unit (AU). Convert CGS to SI and vice versa.
Make a cheat sheet including conversion constants, dimensional formulas, rules of significant figures, and error formulas.
The students can refer to the NCERT Solutions for Class 11 Physics and NCERT Solutions for Class 12 Physics for more learning. It is advisable to also checko NCERT Solutions.
Important Formulas Related to Physics Chapter 1 NCERT Exemplar
Following are the important formulas from units and measurements class 11:
Q is the physical quantity depending on the mass M, time T and length L.
Read Below Related Links
| NCERT Solutions Class 11 and 12 | NCERT Solutions for Class 12 Physics | NCERT Solutions Physics Class 11th |
JEE Mains 2022
JEE Mains 2022
Commonly asked questions
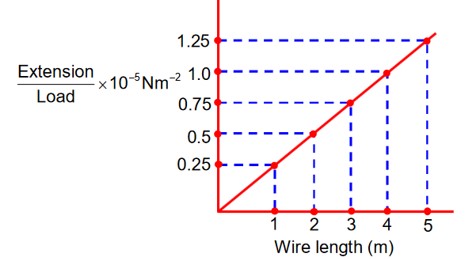
In an experiment to determine the Young’s modulus, steel wires of five different lengths (1, 2, 3, 4, and 5m ) but of same cross section (2 mm2) were taken and curves between extension and load were obtained. The slope (extension / load) of the curves were plotted with the wire length and the following graph is obtained. If the Young’s modulus of given steel wires is x × 1011 Nm-2, then the value of x is________.
Slope =
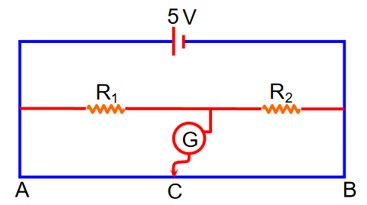
In the given figure of meter bridge experiment, the balancing length AC corresponding to null deflection of the galvanometer is 40 cm. The balancing length, if the radius of the wire AB is doubled, will be__________cm.
Independent of are a is case of uniform wire
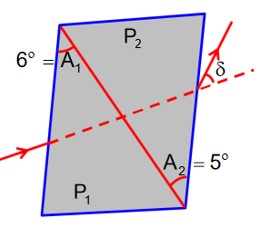
A thin prism of angle 6° and refractive index for yellow light (nY) 1.5 is combined with another prism of angle 5° and nY = 1.55. The combination produces no dispersion. The net average deviation produced by the combination is . The value of x is____________.
A conducting circular loop is placed in X – Y plane in presence of magnetic field in SI unit. If the radius of the loop is 1m. The induced emf in the loop, at time, t = 2s is npV. The value of n is__________.
at t = 2, Eind = 12
As shown in the figure, in steady state, the charge stored in the capacitor is ____________× 10-6C.
A parallel plate capacitor with width 4cm, length 8cm and separation between the plates of 4mm is connected to a battery of 20V. A dielectric slab of dielectric constant 5 having length 1cm, width 4cm and thickness 4mm is inserted between the plates of parallel plate capacitor. The electrostatic energy of this system will be ___________
(Where is the permittivity of free space)
Energy =
A wire of length 30cm, stretched between rigid supports, has it’s nth and (n + 1)th harmonics at 400Hz and 450Hz, respectively, If tension in the string is 2700N, it’s linear mass density is ____________kg/m.
v = 30
A spherical soap bubble of radius 3cm is formed inside another spherical soap bubble of radius 6cm. If the internal pressure of the smaller bubble of radius 3cm in the above system is equal to the internal pressure of the another single soap bubble of radius r cm.
The value of r is___________.
r = 2cm
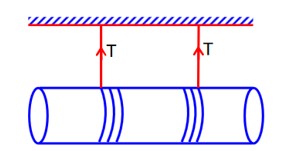
A solid cylinder length is suspended symmetrically through two massless strings, as shown in the figure. The distance from the initial rest position, the cylinder should by unbinding the strings to achieve a speed of 4 ms-1, is__________cm. (take g = 10 ms-2)
.From conservation of energy
mgh =
10 h =
h = 1.2 m = 120 cm
Two inclined planes are placed as shown in figure. A block in Projected from the Point A of inclined plane AB along its surface with a velocity just sufficient to carry it to the top Point B at a height 10m. After reaching the Point B the block slides down on inclined plane BC. Time it takes to reach to the point C from point A is t . The value of t is__________.
(use g = 10 m/s2)
From conservation of Energy
For A to B
T = t1 + t2
Physics NCERT Exemplar Solutions Class 11th Chapter Two Exam