Physics
Get insights from 5.6k questions on Physics, answered by students, alumni, and experts. You may also ask and answer any question you like about Physics
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
8 months agoContributor-Level 10
4.27 No in the both the cases.
A physical quantity which is having both direction and magnitude is not necessarily a vector. For instance, in spite of having direction and magnitude, current is a scalar quantity. The basic necessity for a physical quantity to fall in a vector category is that it ought to follow the “law of vector addition”.
As the rotation of a body about an axis does not follow the basic necessity to be a vector i.e. it does not follow the “law of vector addition”.
New answer posted
8 months agoContributor-Level 10
4.26 Yes and No
A vector in space has no distinct location. The reason behind this is that a vector stays unchanged when it displaces in a way that its direction and magnitude do not change.
A vector changes with time. For instance, the velocity vector of a ball moving with a specific speed fluctuates with time.
Two equivalent vectors situated at different locations in space do not generate the same physical effect. For instance, two equivalent forces acting at different points on a body to rotate the body, but the combination will not generate the equivalent turning effect.
New answer posted
8 months agoContributor-Level 10
(a)
Moment of Inertia of the man-platform system = 7.6 kg-m2
Moment of inertia when the man stretches his hands to a distance 90 cm
= 2 x mr2 = 2 x 5 x (0.9)2 = 8.1 kg-m2
Initial moment of inertia of the system, = 7.6 + 8.1 = 15.7 kg-m2
Angular speed = 30 rev/min
Angular momentum, = = 15.7 x 30 …… (i)
Moment of inertia when the man folds his hands to a distance of 20 cm
= 2 x mmr2= 2 x 5 x (0.2)2 = 0.4 kg-m2
Final moment of inertia, = 7.6 + 0.4 = 8 kg-m2
Final angular speed = and final angular of momentum, = = 8 …… (ii)
From the conservation of a
New answer posted
8 months agoContributor-Level 10
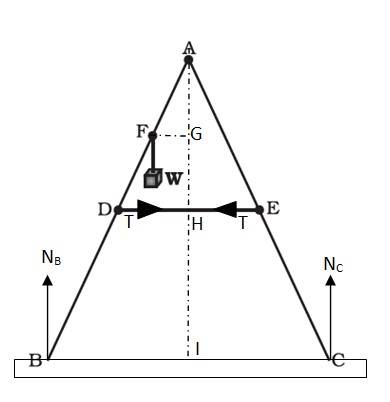
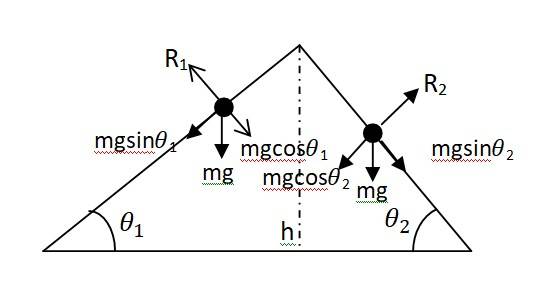
The given situation can be shown as
NB = force exerted on the ladder by the floor point B
NB = force exerted on the ladder by the floor point B
T = Tension in the rope
BA = CA = 1.6 m, DE = 0.5 m and BF = 1.2 m
Mass of the weight, m = 40 kg
The perpendicular drawn from point A on the floor BC, this intersects DE at mid-point H.
Δ ABI and ΔACI are congruent. Therefore BI = IC, I is the mid-point of BC. DE is parallel to BC.
BC = 2 x DE = 1 m and AF = BA – BF = 0.4 m…… (i)
D is the mid-point of AB, hence we can write
AD = (1/2) x BA = 0.8 ……. (ii)
Using equation (i) and (ii), we get FE = 0.4 m
Hence, F is the mid-point of AD.
Hence G will
New answer posted
8 months agoContributor-Level 10
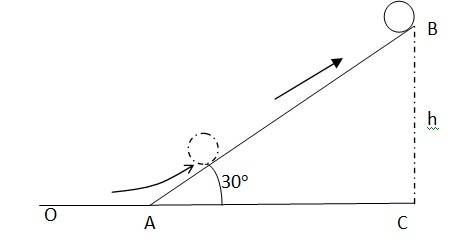
Initial velocity of the cylinder, v = 5 m/s
Angle of inclination, = 30
Height reached by the cylinder = h
Energy of the cylinder at point A:
KE rot + KEtrans
(1/2) I + (1/2) m
Energy of the cylinder at point B = mgh
Using the law of conservation of energy
(1/2) I + (1/2) m = mgh
Moment of inertia of the solid cylinder I = (1/2) mr2
Hence (1/2)(1/2)mr2 + (1/2) m = mgh
We also know v = r
(1/4)m + (1/2) m = mgh
(3/4) = gh
h = (3/4)( = (3/4)(25/9.81) = 1.91 m
In Δ ABC, = , AB = BC / = 3.82 m
Hence the
New answer posted
8 months agoContributor-Level 10
Mass of the oxygen molecule, m = 5.30 * 10-26 kg
Moment of inertia, I = 1.94*10-46 kg m2
Velocity of the oxygen molecule, v = 500 m/s
the separation of atoms in oxygen molecule = 2r.
the mass of each oxygen atom = (m/2)
Moment of inertia I can be calculated as I = (m/2)r2 + (m/2)r2
hence r =
r = sqrt (1.94*10-46 / 5.30 * 10-26 = 6.05 x 10-11
It is given that KErotation = KEtranslation
(1/2)I = (2/3) (1/2)mv2
= (v/r)
= 6.8 x 1012 rad/s
New answer posted
8 months agoContributor-Level 10
Radius of the hoop, r = 2 m, mass of the hoop, m = 100 kg, velocity of the hoop, v = 20 cm /s = 0.2 m/s
Total energy of the hoop = Translational KE + Rotational KE = m +
Moment of inertia about the centre, I = mr2
So the total energy = m +
Since v = r we get
Total energy = m + =
Required work to be done = 100 x 0.2 x 0.2 J = 4 J
New answer posted
8 months agoContributor-Level 10
(a) Let the mass of the sphere = m
Height of the plane = h
Velocity of the sphere at the bottom of the plane = v
At the top of the plane, the total energy of the sphere = potential energy = mgh
At the bottom of the plane, the sphere has both translational and rotational energies.
Hence, total energy = (1/2)mv2 + (1/2)I
Using the law of conservation of energy, we can write: (1/2)mv2+ (1/2)I = mgh …(1)
For a solid sphere, the moment of inertia, I = (2/5)mr2
The equation (1) becomes (1/2)mv2 + (1/2)( (2/5)mr2 = mgh
(1/2) v2 + (1/5)r2 = gh
From the relation v = , we get
(1/2) v2+ (1/5) v2= gh
v =
Since v depends on
New answer posted
8 months agoContributor-Level 10
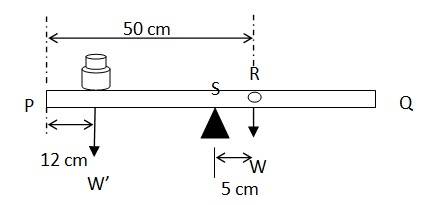
Mass of the meter stick = W
Mass of each coin = 5 g
When the coins are placed 12 cm away from the end P, the centre of mass gets shifted by 5 cm from point R towards the end P. The centre of mass is located at a distance of 45 cm from point P.
The net torque will be conserved for rotational equilibrium about point R,
10 x (45-12) – W' (50-45) = 0
W' = (10 x 33)/5 = 66 g
New answer posted
8 months agoContributor-Level 10
Radius of the original disc = R
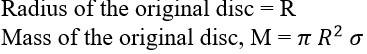
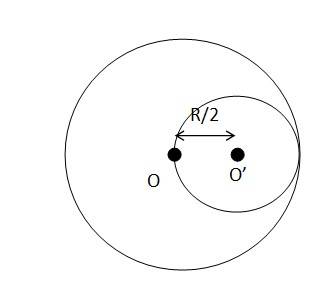
Mass of the smaller disc = = (1/4) = M/4
Let O and O' be the respective centers of the original disc and the cut out disc respectively. As per the definition of the centre of mass, the centre of mass of the original disc is supposed to be concentrated at O, while that of the smaller disc is supposed to be concentrated at O'.
It is given, OO' = R/2
After the smaller disc has been cut from the original, the remaining portion is considered to be a system of two masses. The two masses are
M – concentrated at O and M/4 concentrated at O'
Let x be the distance through which the centers of mas
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 684k Reviews
- 1800k Answers