Ray Optics and Optical Instruments
Get insights from 117 questions on Ray Optics and Optical Instruments, answered by students, alumni, and experts. You may also ask and answer any question you like about Ray Optics and Optical Instruments
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
6 months agoContributor-Level 10
This is a long answer type question as classified in NCERT Exemplar
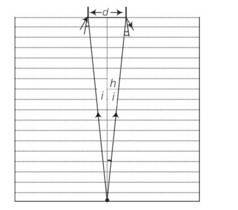
Let d be the diameter of the disc. The spot shall be invisible if the incident rays from the dot at O to the surface at d / 2 at the critical angle.
Let I be the angle of incidence. Using relationship between refractive index and critical angle,
SinC= 1/
= tani
D=
New answer posted
7 months agoContributor-Level 10
9.32 Focal length of the convex lens, = 30 cm
The liquid acts as a mirror, focal length of the liquid =
Focal length of the system (convex lens + liquid), = 45 cm
For a pair of optical systems placed in contact, the equivalent focal length is given as
= + or = -
- 90 cm
Let the refractive index of the lens be and the radius of curvature of one surface be R
Hence, the radius of curvature of the other surface is –R
R can be obtained by using the relation
= ( + ) = (1.5 – 1)(
= , so R =
New answer posted
7 months agoContributor-Level 10
9.31 Angle of deflection, = 3.5
Distance of the screen from the mirror, D = 1.5 m
The reflected rays get deflected by an amount twice the angle of deflection, i.e. 2
The displacement (d) of the reflected spot of light on the screen is given as:
=
d = 1.5 tan 7 = 0.184 m = 18.4 cm
Hence, the deflection of the reflected spot of light is 18.4 cm.
New answer posted
7 months agoContributor-Level 10
9.30 Distance between the objective mirror and the secondary mirror, d = 20 mm
Radius of curvature of objective mirror, = 220 mm
Hence focal length of the objective mirror, = = 110 mm
Radius of curvature of secondary mirror, = 140 mm
Hence focal length of the objective mirror, = = 70 mm
The image of an object placed at infinity, formed by the objective mirror, will act as a virtual object for the secondary mirror. Hence, the virtual object distance for the secondary mirror,
u = = 110 – 20 = 90 mm
Applying the mirror formula for the secondary mirror, we can cal
New answer posted
7 months agoContributor-Level 10
9.29 Focal length of the objective lens, = 140 cm
Focal length of the eyepiece, = 5 cm
Least distance of distinct vision, d = 25 cm
In normal adjustment, the separation between the objective lens and the eyepiece
=
Height of the tower
Distance of the tower (object) from the telescope, u = 3 km = 3000 m
The angle subtended by the tower at the telescope is given as : = = rad
The angle subtended by the image produced by the objective lens is given as , where = height of the image of the tower formed by the objective lens
So, = = &nbs
New answer posted
7 months agoContributor-Level 10
9.28 Focal length of the objective lens, = 140 cm
Focal length of the eyepiece, = 5 cm
Least distance of distinct vision, d = 25 cm
When the telescope is in normal adjustment, its magnifying power is given as:
= = = 28
When the final image is formed at d, the magnifying power of the telescope is given as:
= ] = 28 ] = 33.6
New answer posted
7 months agoContributor-Level 10
9.27 Focal length of the objective lens, = 1.25 cm
Focal length of the eyepiece, = 5 cm
Least distance of distinct vision, d = 25 cm
Angular magnification of the compound microscope = 30X
Total magnifying power of the compound microscope, m = 30
The angular magnification of the eyepiece is given by the relation:
= (1 + ) = (1 + = 6
The angular magnification of the objective lens ( ) is related to by the equation
m = or
= = = 5
We also have relation
5 = or ……….(1)
Applying lens formula for the objective lens
&nbs
New answer posted
7 months agoContributor-Level 10
9.26 Though the image size is bigger than the object, the angular size of the image is equal to the angular size of the object. A magnifying glass helps one see the object placed closer than the least distance of distinct vision (i.e. 25 cm). A closer object causes a larger angular size. A magnifying glass provides angular magnification. Without magnification, the object cannot be placed closer to the eye. With magnification, the object can be placed much closer to the eye.
Yes, the angular magnification changes. When the distance between the eye and a magnifying glass is increased, the angular magnification decreases a little. This is
New answer posted
7 months agoContributor-Level 10
9.25 Area of the virtual image of each square, A = 6.25
Area of each square, = 1
Hence the linear magnification of the object can be calculated as:
m = = = 2.5, but m = or v = 2.5u
Focal length of the magnifying glass, f = 10 cm. According to lens formula
= -
= - or . Hence u = -6 cm and v = -15 cm
The virtual image is formed at a distance of 15 cm, which is less than the near point (i.e. 25 cm) of a normal eye. Hence, it cannot be seen by the eyes directly.
New answer posted
7 months agoContributor-Level 10
9.24 The maximum possible magnification is obtained when the image is formed at the near point (d = 25 cm)
Image distance, v = -d = -25 cm
Focal length, f = 10 cm
Object distance = u
According the lens formula, we have:
= -
= - = -
u = - 7.14 cm
Hence, to view the squares distinctly, the lens should be kept 7.14 cm away from them.
Magnification= =
Magnifying power = = = 3.50
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 680k Reviews
- 1800k Answers