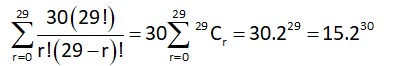Relations and Functions
Get insights from 125 questions on Relations and Functions, answered by students, alumni, and experts. You may also ask and answer any question you like about Relations and Functions
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
4 months agoContributor-Level 10
18 = 32 * 2
For G.C.D to be 3. no. of four digits should be only multiple of 3, but not multiple of 9 & also should not be even.
As we know no. of the form 9 k -> 1000
9 k + 1 -> 1000
9 k + 2 -> 1000
9 k + 3 -> 1000 -> Total no. = 2000
9 k + 4 -> 1000
9 k + 5 -> 1000
9 k + 6 ->1000
9 k + 7 -> 1000
9 k + 8 -> 1000
In which half will be even & half be odd so Required no. = 1000
New answer posted
4 months agoNew answer posted
5 months agoContributor-Level 10
For limit to exist a - b = 0 . (i),
and . (iii)
Solving (i), (ii) and (iii) we get α = 6, β = 6 and
New answer posted
5 months agoContributor-Level 10
Case 1 : If f (3) = 3 then f (1) and f (2) take 1 or 2
No. of ways = 2.6 = 12
Case 2 : If f (3) = 5 then f (1) and f (2) take 2 or 3
OR 1 and 4
No. of ways = 2.6.2 = 24
Similarly for all other cases
Total no. of ways 90.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers