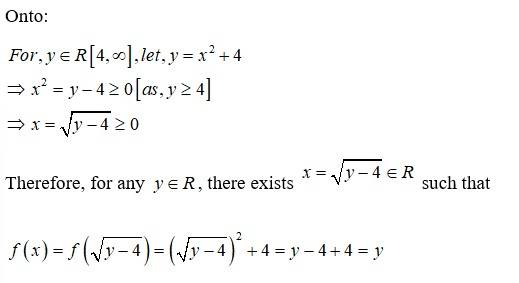Relations and Functions
Get insights from 125 questions on Relations and Functions, answered by students, alumni, and experts. You may also ask and answer any question you like about Relations and Functions
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
Let be an invertible function.
Also, suppose f has two inverses (say g1 and g2 ).
Then, for all y ∈ Y, we have:
[f is invertible => f is one-one]
[g is one-one]
Hence, f has a unique inverse.
New answer posted
7 months agoContributor-Level 10
is given by,
f is a one-one function.
Onto:
Therefore, for any , there exists such that
f is onto.
Thus, f is one-one and onto and therefore, exists.
Let us define by
Hence, f is invertible and the inverse of f is given by
New answer posted
7 months agoContributor-Level 10
is given as
f is a one-one function.
It is clear that Range f is onto.
Range f is one-one onto and therefore, the inverse of the function:
Range f exists.
Let g: Range be the inverse of f.
Let y be an arbitrary element of range f.
Since Range f is onto, we have:
New answer posted
7 months agoContributor-Level 10
(i) f: {1, 2, 3, 4} → {10} defined as:
f = { (1, 10), (2, 10), (3, 10), (4, 10)}
From the given definition of f, we can see that f is a many one function as: f (1) = f (2) = f (3) = f (4) = 10
∴f is not one-one.
Hence, function f does not have an inverse.
(ii) g: {5, 6, 7, 8} → {1, 2, 3, 4} defined as:
g = { (5, 4), (6, 3), (7, 4), (8, 2)}
From the given definition of g, it is seen that g is a many one function as: g (5) = g (7) = 4.
∴g is not one-one,
Hence, function g does not have an inverse.
(iii) h: {2, 3, 4, 5} → {7, 9, 11, 13} defined as:
h = { (2, 7), (3, 9), (4, 11), (5, 13)}
It is seen that
New answer posted
7 months agoContributor-Level 10
It is given that
Therefore for all
Hence, the given function f is invertible and the inverse of f is itself.
New question posted
7 months agoNew answer posted
7 months agoContributor-Level 10
The functions f: {1, 3, 4} → {1, 2, 5} and g: {1, 2, 5} → {1, 3} are defined as
f = { (1, 2), (3, 5), (4, 1)} and g = { (1, 3), (2, 3), (5, 1)}.
gof (1) = g (f (1) = g (2) = 3 [f (1) = 2 and g (2) = 3]
gof (3) = g (f (3) = g (5) = 1 [f (3) = 5 and g (5) = 1]
gof (4) = g (f (4) = g (1) = 3 [f (4) = 1 and g (1) = 3]
gof = { (1, 3), (3, 1), (4, 3)}
New answer posted
7 months agoContributor-Level 10
Given, defined as
For such that
So, is one-one
And for , there exist such that
is onto
Hence, option (A) is correct.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers