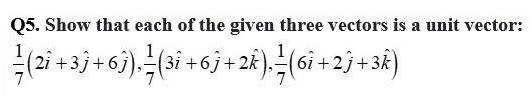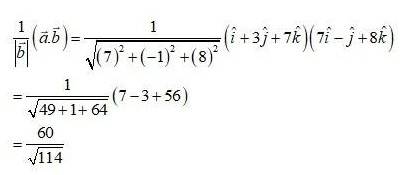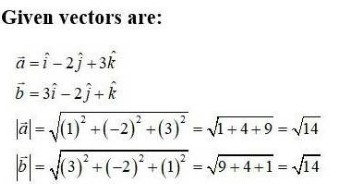Vector Algebra
Get insights from 133 questions on Vector Algebra, answered by students, alumni, and experts. You may also ask and answer any question you like about Vector Algebra
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
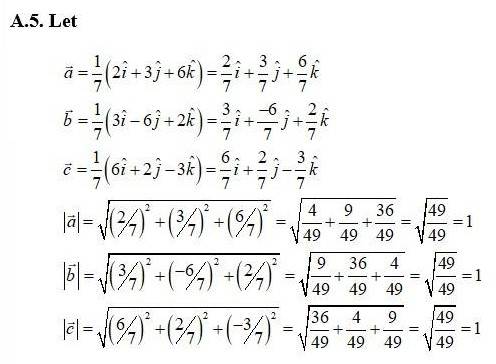
Here, each of the given three vector is a unit vector.
Therefore, the given three vectors are mutually perpendicular to each other.
New answer posted
7 months agoContributor-Level 10
Let,
The projection of vector on is given by,
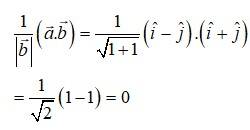
The projection of vector on is 0.
New answer posted
7 months agoContributor-Level 10
We know,
If and are two collinear vector, they are parallel.
So,
Hence, the respective component are proportional but, vector and can have different direction.
Thus, the statement given in D is incorrect.
The correct answer is D.
New answer posted
7 months agoContributor-Level 10
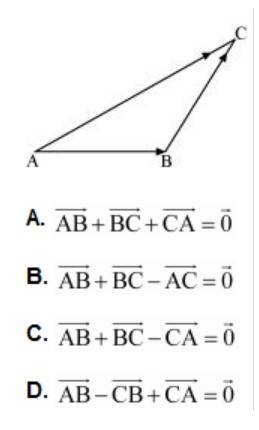
(A)
By triangle law of addition in given triangle, we get:
So, (A) is true.
(B)
So, (B) is true.
(C)
The eQ.uation in alternative C , which is not true, is incorrect.
(D)
The, equation given is alternative is D is true.
The correct answer is C.
New answer posted
7 months agoContributor-Level 10
We have,
Now,
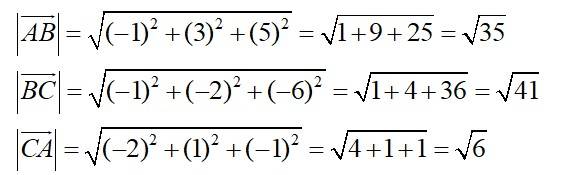
Hence,
Hence, given points from the vertices of a right angled triangle.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers