Vector Algebra
Get insights from 133 questions on Vector Algebra, answered by students, alumni, and experts. You may also ask and answer any question you like about Vector Algebra
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
Let, be two unit vectors and be the angle between them.
Then,
Now, is a unit vector if
[ is unit vector.]
Therefore, the correct answer is (D)
New answer posted
7 months agoContributor-Level 10
Let, in triangle between two vector
Then, without loss of generality, are non-zero vector so that
are positive.
We know,
So,
Therefore, , when
Hence, the correct answer is B.
New answer posted
7 months agoContributor-Level 10
( Distributive of scalar product over addition )
( Scalar product is commutative , )
Therefore, are perpendicular.
New answer posted
7 months agoContributor-Level 10
Given that are mutually perpendicular vectors, we have
Let, vector be inclined to at angles, respectively.
Therefore, the vector are equally inclined to
New answer posted
7 months agoContributor-Level 10
The unit vector along is given as;
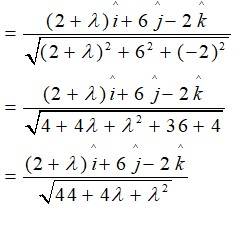
By Q.uestion, scalar product of with this unit vector is 1.
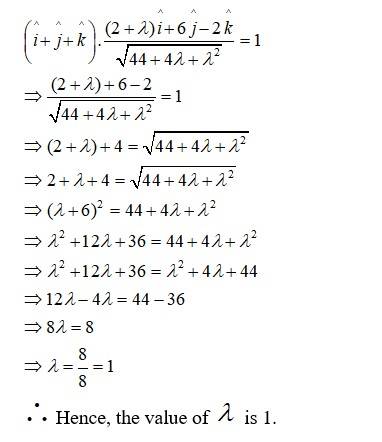
New answer posted
7 months agoContributor-Level 10
Given,
Let,
Since, is perpendicular to both
We know,
Putting this value in (3) we get
Putting value in (2), we get
The reQ.uired vector is
New answer posted
7 months agoContributor-Level 10
Given,
Adjacent sides of parallelogram are
Diagonal of parallelogram =
Thus, the unit vector parallel to diagonal
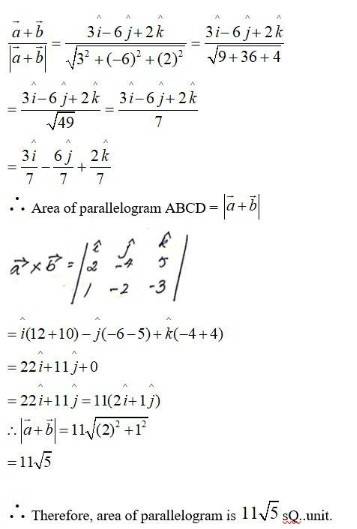
New answer posted
7 months agoContributor-Level 10
Given,
It is given that point R divides a line segment joining two points P and Q.
externally in the ratio 1:2 Then,
Position vector of the mid-point of RQ.
New answer posted
7 months agoContributor-Level 10
Given,
Now,

Thus, A,B and C are collinear.
Let, be the ratio that point B divides AC.
We have,
On eQ.uating the corresponding component , we get
Hence, point B divides AC in the ratio
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers