Chemical Kinetics

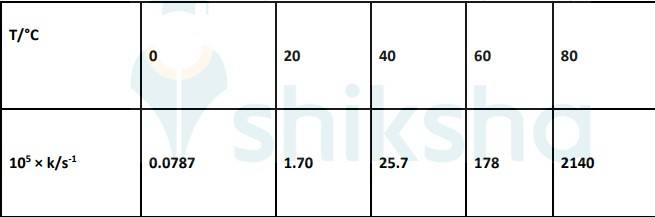
4.31 To convert the temperature in °C to °K we add 273 K.

The graph is given as:

The Arrhenius equation is given by k = Ae^-Ea/RT

Where, k- Rate constant

A- Constant

E_a-Activation Energy

R- Gas constant

T-Temperature

Taking natural log on both sides,

ln k = ln A- (E_a/RT). equation 1

By plotting a graph, ln K Vs 1/T, we get y-intercept as ln A and Slope is –E_a/R.

Slope = (y₂-y₁)/ (x₂-x₁)

By substituting the values, slope = -12.301

? –E_a/R = -12.301

But, R = 8.314 JK^-1mol^-1

? _aE= 8.314 JK^-1mol^-1 * 12.301 K

? _aE= 102.27 kJ mol^-1

Substituting the values in equation 1 for data at T = 273K

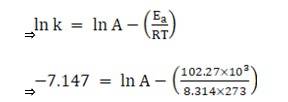
(? At T = 273K, ln k =-7.147)

On solving, we get ln A = 37.911

? A = 2.91*10⁶

When T = 30⁰C, hence T = 30 + 273 = 303K

? ln k =-2.8

? k = 6.08x10^-2s^-1.

When T = 50⁰C, hence T = 50 + 273 = 323K

Substituting in equation 1,

A = 2.91 * 10⁶, E_a = 102.27 kJ mol^-1

Ln K = ln (2.91 * 10⁶)- 102.27/ (8.314 * 323)

Thus, ln k = -0.5 and k = 0.607s^-1.

4.30 When t = 0, the total partial pressure is P₀ = 0.5 atm

When time t = t, the total partial pressure is P_t = P₀ + p

P₀-p = P_t-2p, but by the above equation, we know p = P_t-P₀

Hence, P₀-p = P_t-2 (P_t-P₀)

Thus, P₀-p = 2P₀ – P_t

We know that time

t= 2.303/K log R₀ / R

Where, k- rate constant

[R]_° -Initial concentration of reactant [R]-Concentration of reactant at time 't'

Here concentration can be replaced by the corresponding partial pressures.

Hence, the equation becomes,

t= 2.303/K log P₀ / P₀ - P

t= 2.303/K log P₀ / 2P₀ - P_t

? equation 1

At time t = 100 s, P_t = 0.6 atm and P₀ = 0.5 atm,

Substituting in equation 1,

100 = 2.303/k log 0.5 / (2X0.5) - 0.6

Thus, k = 2.231 * 10^-3 s^-1

The rate of reaction R = k * P_S02Cl₂

When total pressure P_t = 0.65 atm and P₀ = 0.5 atm, then

[P_S02Cl₂ = 2P₀-P_t

Thus, substituting the values, P_S02Cl₂ = 2 (0.5)-0.6 = 0.35 atm

R = k * P_S02Cl₂ = 2.231 * 10^-3 s^–1 * 0.35

Rate of the reaction R = 7.8 * 10^-4atm s^–1

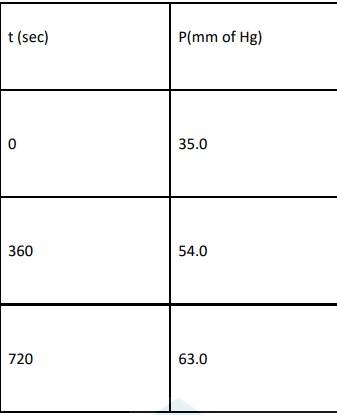
4.29 When t = 0, the total partial pressure is P₀ = 35.0 mm of Hg

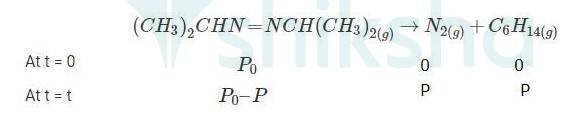
When time t = t, the total partial pressure is P_t = P₀ + p

P₀-p = P_t-2p, but by the above equation, we know p = P_t-P₀ Hence, P₀-p = P_t-2 ( P_t-P₀)

Thus, P₀-p = 2P₀ – P_t

We know that time

t= 2.303/K log R₀ / R

Where, k- rate constant

[R]_° -Initial concentration of reactant

[R]-Concentration of reactant at time 't'

Here concentration can be replaced by the corresponding partial pressures.

Hence, the equation becomes,

t= 2.303/K log P₀ / P₀ - P

t= 2.303/K log P₀ / 2P₀ - P_t

? equation 1

At time t = 360 s, P_t = 54 mm of Hg and P₀ = 30 mm of Hg, Substituting in equation 1,

360 = 2.303/k log 30 / (2X30)-54

k= 2.175 X 10^-3 s^-1

At time t = 720 s, P_t = 63 mm of Hg and P₀ = 30 mm of Hg, Substituting in equation 1,

720 = 2.303 / k log 30 / (2X30) - 63

Thus, k = 2.235 * 10^-3 s^–1

Taking average, k = (2.235 * 10^-3 s^–1 + 2.175 * 10^-3 s^–1)/2

? k = 2.21 * 10^-3 s^–1.

4.27 Let, initial concentration be [R]_°

Concentration at 90% completion be (100-90)/100)* [R]_°

? Concentration at 90% be 0.1 [R]_°

Concentration at 99% completion be (100-99)/100)* [R]_°? Concentration at 99% be 0.01 [R]_°

_{we know time, t= 2.303/K log R0 / R}

Time taken for 90% completion is 

T₉₀ = 2.303 / K log R₀ / 0.1 R₀ 

T₉₀ = 2.303 / K log 1 / 0.1

T₉₀ = 2.303 / K log 10 / 1

T₉₀ = 2.303 / K

Time taken for 99% completion is

T₉₉ = 2.303 / K log R₀ / 0.01 R₀ 

T₉₉ = 2.303 / K log 1 / 0.01

T₉₉ = 2.303 / K log 100 / 1

T₉₉ = 2 X 2.303 / K

T₉₉ = 2 T₉₀

Hence, the time taken to complete 9% of the first order reaction is twice the time required for the completion of 90% of the reaction.

4.26 Initial concentration, [R]_° = 1? g

Final concentration, [R] Half-life t_1/2 = 28.1 years Solution:

We know, t_1/2 = 0.693/k Where, k – rate constant

? k = 0.693/ t_1/2

? k = 0.693/ (28.1 yrs)

? k = 0.0246 yrs^-1

Also, t = 2.303 / k log R₀ / R

If t = 10yrs, then, using the formula, we get,

t = 2.303 / k log R₀ / R

10 = 2.303 / 0.0246 log 1 / R₁₀ 

log 1 / R₁₀  = 0.0246 X 10 / 2.303

log 1 / R₁₀ = 0.246 / 2.303

1 / R₁₀ = antilog (0.246 / 2.303)

1 / R₁₀ = 1.278    

?   R₁₀ = 0.7824? g

If t = 60yrs, then again, we get,

60 = 2.303 / 0.0246 log 1 / R₆₀ 

log 1 / R₆₀  = 0.0246 X 60 / 2.303

log 1 / R₆₀ = antilog (1.476 / 2.303)

1 / R₆₀ = 4.374   

? [R]₆₀ = 0.228? g

?0.2278? g of ⁹⁰Sr will be left after 60 years.