Class 11th
Get insights from 8k questions on Class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
8 months agoContributor-Level 10
41. Given, n (X)= 17
n (Y) = 23
n (X Y)= 38.
So, n (X Y) = n (X) + n (Y) n (X Y)
n (X Y) = n (X) + n (Y) n (X Y)
= 17 + 23 38.
= 2
New answer posted
8 months agoContributor-Level 10
40. (i) A A = U
(ii) ∩ A = U ∩ A = A.
(iii) A ∩ A = .
(iv) U ∩ A = ∩ A = .
New answer posted
8 months agoContributor-Level 10
39. A = U – A
= Set of all triangle in a plane - Set of all triangle with at least the angle different from 60°.
= Set of all triangle with each angle 60°.
A? = set of all equilateral triangle.
New answer posted
8 months agoContributor-Level 10
38. (i) (A B) = U – (A B)
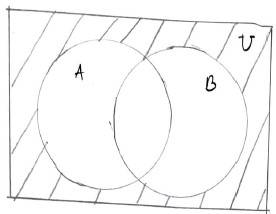
(ii) A ∩ B = (AU B) = U – (AU B)
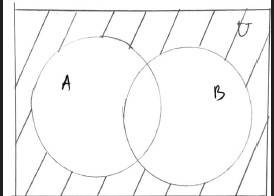
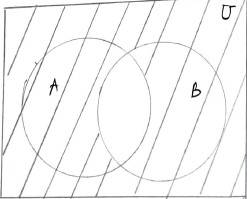
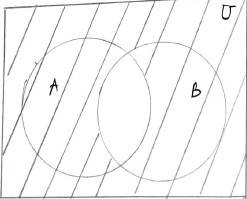
New answer posted
8 months agoContributor-Level 10
37. (i) L.H.S = (A B) = U – (A B)
= {1,2,3,4,5,6,7,8,9} – [ {2,4,6,8) {2,3,5,7}]
= {1,2,3,4,5,6,7,8,9} – {2,3,4,5,6,7,8}
= {1,9}
R.H.S. = A ∩ B = [U – A] ∩ [U B]
= ∩
= {1,3,5,7,9} ∩ {1,4,6,8,9}
= {1,9}
? L.H.S. = R.H.S.
(A B) = A ∩ B.
(ii) L.H.S. = (A ∩ B) = U – (A ∩ B)
= {1,2,3,4,5,6,7,8,9} – [ {2,4,6,8} ∩ {2,3,5,7}]
= {1,2,3,4,5,6,7,8,9} – {2}
= {1,3,4,5,6,7,8,9}
R.H.S. = A B
= [U – A] [U – B]
= [ {1,2,3,4,5,6,7,8,9} – {2,4,6,8}] [ {1,2,3,4,5,6,7,8,9} – {2,3,5,7}]
= {1,3,5,7,9} {1,4,6,8,9}
= {1,3,4,5,6,7,8,9}
? L.H.S. = R.H.S.
(A ∩ B) = A B.
New answer posted
8 months agoContributor-Level 10
3. (i) {x : x is an odd natural number}
(ii) {x : x is an even natural number}
(iii) {x : x is not a multiple of 3}
(iv) {x : x is a positive composite number and x = 1}
(v) {x : x is a natural number not divisible by 3 and 5}.
(vi) {x : x is not a perfect square}
(vii) {x : x is not a perfect cube}
(viii) We have, x + 5 = 8.
x = 8 – 5 = 3
x = 3
? {x : x ≠ 3, x? N}
(ix )We have,
2x + 5 = 9
2x = 9 – 5
2x = 4
x = 2
? {x : x? N and x ≠ 2}
(x) {x : x < 7} = {1,2,3,4,5,6}
(xi) We have,
2x + 1 >10
2x >10 – 1
x >
? = {1,2,3,4}
New answer posted
8 months agoContributor-Level 10
35. (i) A = U – A = {a, b, c, d, e, f, g, h} – {a, b, c}
= {d, e, f, g, h}
(ii) B = U – B = {a, b, c, d, e, f, g, h} – {d, e, f, g}
= {a, b, c, h}.
(iii) C = U – C = {a, b, c, d, e, f, g, h} – {a, c, e, g}.
= {b, d, f, h}
(iv) D = U – D = {a, b, c, d, e, f, g, h} – {f, g, h, a}
= {b, c, d, e}
New answer posted
8 months agoContributor-Level 10
34. (i) A = U – A = {1,2,3,4,5,6,7,8,9} – {1,2,3,4}
= {5,6,7,8,9}
(ii) B = U – B = {1,2,3,4,5,6,7,8,9} – {2,4,6,8}
= {1,3,5,7,9}.
(iii) (A C) = A ∩ C
= {5,6,7,8,9} ∩ [U – C] [? (i)]
= {5,6,7,8,9} ∩ [ {1,2,3,4,5,6,1,8,9} – {3,4,5,6}]
= {5,6,7,8,9} ∩ {1,2,7,8,9}
= {7,8,9}
(iv) A B) = A ∩ B [By demorgan's law]
= {5,6,7,8,9} ∩ {1,3,5,7,9} [? (i) and (ii)]
= {5,7,9}.
(v) (A) = U – A = {1,2,3,4,5,6,7,8,9} – {5,6,7,8,9} [? (1)]
= {1,2,3,4} = A
(A) = A.
(vi) (B – C) = U – (B – C) = {1,2,3,4,5,6,7,8,9} – [ {2, 4, 6, 8} – {3, 4, 5, 6}]
= {1,2,3,4,5,6,7,8,9} – {2,8}
= {1,3,4, 5, 6,7,9}.
New answer posted
8 months agoContributor-Level 10
20. Let P have the coordinates (x, y, z)
Then,
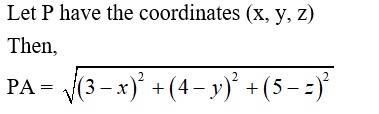
=
=
=
=
And,
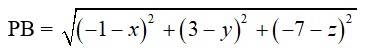
=> =
=
=
=
=
The equation of P such that,
=> +
=>
=>
=> =
New answer posted
8 months agoContributor-Level 10
19. Given, x-coordinate of R = 4
Let R divides line segment joining points P(2, –3, 4) and Q(8, 0,10) internally in the ratio k : 1. Then coordinate of R is
=
Then,
= 4
=>
=>
=>
=>
=>
=>
Hence,
=
=
=
=
And,
z =
=
=
=
= 6
Therefore, coordinates of R is (4, –2, 6).
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
