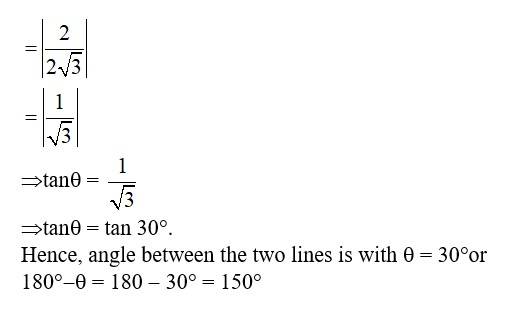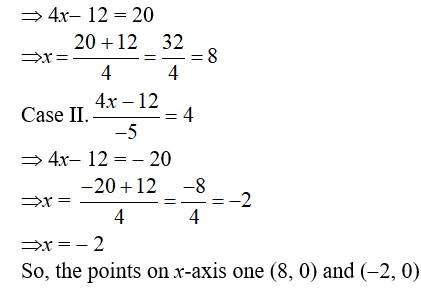Class 11th
Get insights from 8k questions on Class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
8 months agoNew answer posted
8 months agoContributor-Level 10
44.
The slope of line x- 7y + 5 = 0 is
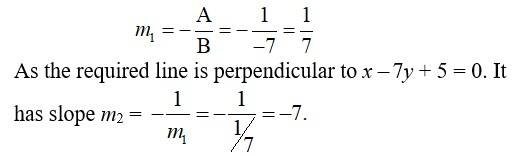
So, equation of line with slope m2 and having x-intercept 3 is
y = m (x-d), d = x- intercept
⇒y = - 7 (x- 3)
⇒y = - 7x + 21
⇒ 7x + y- 21 = 0.
New answer posted
8 months agoContributor-Level 10
43.
The slope of the line 3x - 4y + 2 = 0 is,
So, slope of line parallel to 3x - 4y + 2 = 0 is also m=
Hence, this parallel line passes through ( -2, 3) we can write,
3 (x + 2) = 4 (y - 3)
3x + 6 = 4y - 12
3x - 4y + 6 + 12 = 0.
3x - 4y + 18 = 0. Which is the required equation of line.
New answer posted
8 months agoContributor-Level 10
42.
(i) Given, equation of lines are
15x + 8y- 34 = 0
15x + 8y + 31 = 0
So, c1 = 34 and c2 = 31, A = 15 and B = 8

New answer posted
8 months agoContributor-Level 10
19. Given, R= { (a, b): a, b
We know that, the difference of two integers is also an integer.
R= { (a, b): a – b
Domain of R=Z.
Range of R= Z.
New answer posted
8 months agoContributor-Level 10
18. Given, A={x, y, z}so, n(A)=3
B={1,2} so n(B)=2
? n(A * B)=n(A) *n(B)=3 * 2=6
Hence, no. of relation from A to B=Number of subsets of A * B
=26
=64.
New answer posted
8 months agoContributor-Level 10
17. GivenR= { (x, x3) : x is a prime number less than 10}
R = { (x, x3) : x = 2,3,5,7}
= { (2,23), (3,33), (5,53), (7,73)}
= { (2,8), (3,27), (5,125), (7,343)}
New answer posted
8 months agoContributor-Level 10
40.
The given equation of the line is.
12 (x + 6) = 5 (y- 2)
⇒ 12x + 72 = 5y- 9
⇒ 12x- 5y + 72 + 9 = 0
⇒ 12x- 5y + 82 = 0
The perpendicular distance of point (-1, 1) from the line is given by
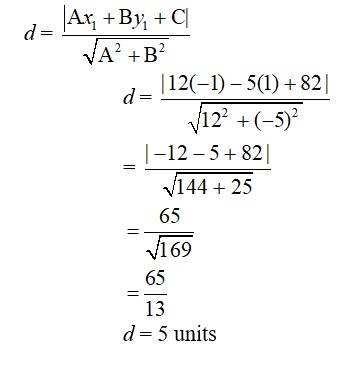
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers