Class 11th

Initial volume, $V_1$ = 100 lit = 100 $*{10}^{-3}$ $m^3$

Final volume, $V_2$ = 100.5 lit = 100.5 $*{10}^{-3}$ $m^3$

Increase in volume, ΔV = $V_2-V_1$ = 0.5 $*{10}^{-3}$ $m^3$

Increase in pressure, ΔP = 100 atm = 100 $*$ 1.013 $*{10}^{5}Pa$

Bulk modulus, k = $V_1\frac{\mathrm{\Delta }\mathrm{P}}{\mathrm{\Delta }\mathrm{V}}$ = $\frac{100\mathrm{}*{10}^{-3}*100\mathrm{}*1.013*{10}^5}{0.5\mathrm{}*{10}^{-3}}$ Pa = 2.026 $*{10}^9$ Pa

Bulk modulus of air = 1.0 $*{10}^{5}Pa$

(Bulk modulus of water / Bulk modulus of air) = (2.026 $*{10}^9)/$ 1.0 $*{10}^5$ = 2.026 $*{10}^4$

This higher ratio is attributed to the higher compressibility of air than water.

Mass, m = 14.5 kg

Length of the steel wire, l = 1.0 m

Angular velocity,  $\omega$ = 2 rev/s

Cross sectional area of the wire, A = 0.065 ${cm}^2$ = 0.065 $*{10}^{-4}{m}^2$

Let Δl be the elongation of the wire

When the mass is placed at the position of the vertical circle, the total force on the mass is

F = mg + ml ${\omega }^2$ = 14.5 $*\left(9.81+1*2^2\right)$ = 200.25 N

Young's modulus for steel,  $Y_s$ = Stress / Strain = 2 $*{10}^{11}$ Pa

Stress = F/A = 200.25/0.065 $*{10}^{-4}$

Strain = (Δl/l) = (Δl/1) = Δl

Δl = (200.25/0.065 $*{10}^{-4})/$ 2 $*{10}^{11}$ = 1.54 $*{10}^{-4}$ m

It is given that the tension, F in each wire is same. Since the wire is of same length, Strain also will be same.

If $d_c$ is the diameter of copper wire and Young's modulus of copper $Y_c$ = 110 $*{10}^{9}Pa$ and strain is s, then $Y_c$ = $\frac{F}{\frac{\pi }{4}{d_c}^2}$ , $d_c=\sqrt{\frac{4F}{\pi *Y_c}}$

Similarly, if $d_i$ is the diameter of iron wire and $Y_i$ is the Young's modulus of iron = 190 $*{10}^{9}Pa$ , then $d_i$ = $\sqrt{\frac{4F}{\pi *Y_i}}$

$\frac{d_c}{d_i}$ = $\sqrt{\frac{Y_i}{Y_c}}$ = $\sqrt{\frac{190}{110}}$ = 1.314

Area of cross-section, A = $\pi {1.5}^2$ ${cm}^2$ = 7.07 $*{10}^{-4}{m}^2$

Maximum stress = Maximum load / cross sectional area

Maximum load = Maximum stress $*$ cross sectional area = 108 $*$ 7.07 $*{10}^{-4}$ = 7.07 $*{10}^4$ N

Area of cross-section, A = 15.2 mm $*19.1\mathrm{m}\mathrm{m}$ = 15.2 $*19.1*{10}^{-6}{\mathrm{m}}^2=2.9\mathrm{}*{10}^{-4}{\mathrm{m}}^2$

Force, F = 44500 N

Stress, F/A = (44500/$2.9\mathrm{}*{10}^{-4})$ N/ ${\mathrm{m}}^2$

Modulus of elasticity,  $\eta$ = Stress / Strains, Strains = Stress / $\eta$

For copper,  $\eta$ = 42$*{10}^9$ $\mathrm{N}/{\mathrm{m}}^2$

Strains = (44500/$2.9\mathrm{}*{10}^{-4})/($ 42 $*{10}^9)$ = 3.65 $*{10}^{-3}$

Mass of the big structure, M = 50000 kg = 50000 $*9.8N$ = 4.9 $*{10}^5$ N

Inner radius of the column, r = 30 cm = 0.3 m

Outer radius of the column, R = 60 cm = 0.6 m

Young's modulus of steel, Y = 2 $*{10}^{11}$ Pa

Total force exerted on 4 columns, F = 4.9 $*{10}^5$ N

Force exerted on single column, f = F/4 = 1.225 $*{10}^5$ N

Cross sectional area of each column, A = $\pi (R^2-r^2)$ = $\pi ({0.6}^2-{0.3}^2)$ = 0.848 $m^2$

Stress in each column = f/A

Young's modulus, Y = Stress / Strain, Strain = Stress / Y = f/ (A $*Y)$ = $\frac{1.225\mathrm{}*{10}^5}{0.848*2*{10}^{11}}=7.22*{10}^{-7\mathrm{}}$ m

Edge of the aluminium cube, L = 10 cm = 0.1 m, Area A = 0.01 $m^2$

Mass attached, m = 100 kg = 100 $*$ 9.8 = 980 N = Applied force F

Shear modulus $\eta$ = 25 GPa = 25 $*{10}^{9}Pa$

Shear modulus $\eta$ = Shear stress / Shear strain = $\frac{\frac{F}{A}}{\frac{?L}{L}}$ ,  $?L=\frac{F*L}{\eta *A}$ = $\frac{980*0.1}{25\mathrm{}*{10}^9*0.01}$ = 3.92 $*{10}^{-7}m$

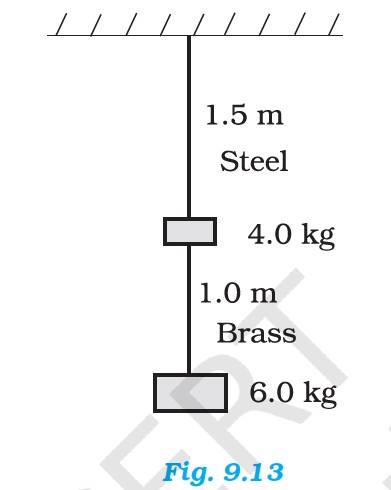
Diameter of wires, d = 0.25 cm, radius, r = 0.125 cm

Cross-sectional area, $A_1$ = $A_2$ = $\pi *r^2=0.049{cm}^2$ = 4.908 $*{10}^{-6}$ $m^2$

Length of the steel wire, $L_1=1.5\mathrm{}\mathrm{m}$ , length of the brass wire, $L_2=1.0\mathrm{}\mathrm{m}$

Change in length of the steel wire $=?L_1,$ Change in length of the copper wire $=?L_2$

Total force exerted on the steel wire, $F_1$ = ( 4+6) kg = 10 kg = 98 N

Young's modulus of steel , $Y_1$ = $\frac{\frac{F_1}{A_1}}{\frac{?L_1}{L_1}}$ = 2.0 $*{10}^{11}$ Pa

$?L_1$ = $\frac{F_1}{A_1}*\frac{L_1}{Y_1}=\mathrm{}\frac{98*1.5}{4.908*{10}^{-6}*2.0*{10}^{11}}$ = 1.497 $*{10}^{-4}$ m

Similarly for brass wire, $F_2$ = 6 kg = 58.8 N, $Y_2$ = $0.91*{10}^{11}\mathrm{}\mathrm{P}\mathrm{a}$

$?L_2$ = $\frac{F_2}{A_2}*\frac{L_2}{Y_2}=\mathrm{}\frac{58.8*1.0}{4.908*{10}^{-6}*0.91*{10}^{11}}$ = 1.316 $*{10}^{-4}$ m

For a given stress, the strain in rubber is more than it is in steel, hence the Young's modulus of rubber is lesser than in steel. So the statement is False.

Shear modulus is the ratio of the applied stress to the change in the shape of a body. The stretching of a coil changes its shape. Hence, shear modulus of elasticity is involved in this process.

 = 2.2 $*{10}^{-4}{m}^3$

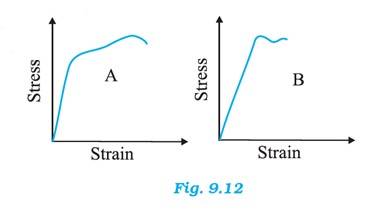
Material A has greater Young's modulus.

Material A is the strongest as it can withstand more strain than material B without fracture.