Class 11th
Get insights from 8k questions on Class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
8 months agoContributor-Level 10
Mass of the string, M = 2.5 kg
Tension in the string, T = 200 N
Length of the string, l = 20 m
Mass per unit length, = = = 0.125 kg/m
The velocity (v) of the transverse wave in the string is given by the relation:
= = 40 m/s
Therefore, time taken by the disturbance to reach the other end, t = = = 0.5 s
New answer posted
8 months agoContributor-Level 10
Water pressure at the bottom, p = 1.1 Pa
Initial volume of the steel ball, V = 0.32
Bulk modulus of the steel, B = 1.6 N/
The ball falls at the bottom of the Pacific ocean which is 11 km beneath the surface
Let the change in volume of the ball on reaching the bottom of the trench be ΔV
We know, bulk modulus, B = or ΔV =
ΔV = = 2.2
New answer posted
8 months agoContributor-Level 10
Diameter of the metal strip, d = 6.0 mm = 6 m
Radius, r = d/2 = 3 m
Maximum shearing stress = 6.9 Pa =
Maximum force = Maximum stress
= 6.9 = 6.9 = 1950.93 N
Since each rivet carries 1/4th of load,
Maximum tension on each rivet = 4 N = 7803.72 N
New answer posted
8 months agoContributor-Level 10
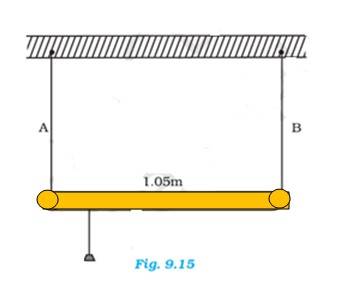
Length of the mild steel wire, l = 1.0 m
Area of cross-section, A = 0.5 = 0.5
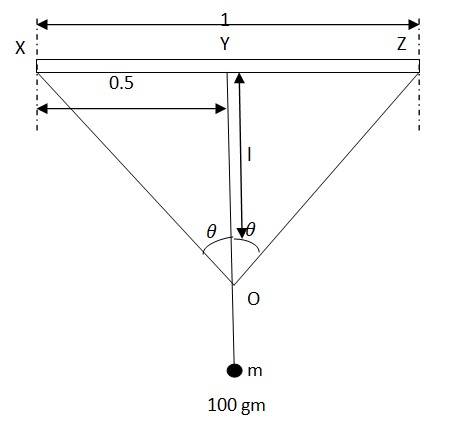
A mass of 100 gm is suspended at the midpoint.
m = 100 gm= 0.1 kg
Due to the weight, the wire dips, as shown in the figure.
Original length = XZ, depression = l
The final length of the wire after it dips = XO + OZ
Increase in length of the wire, Δl = (XO + OZ) – XZ ……(i)
From Pythagoras theorem
XO = OZ =
From equation (i)
Δl = 2 - 1.0 = 2 - 1.0 = - 1.0
Neglecting the smaller terms, we can write, Δl =
We know, Strain =
Let T be the tension in the wire, then
mg = 2T
From the figure
=&
New answer posted
8 months agoContributor-Level 10
Cross-sectional area of wire A, = 1 = 1
Cross-sectional area of wire B, = 2 = 2
Young's modulus for steel, = 2 N/
Young's modulus for aluminium, = 7 N/
Stress in the wire = =
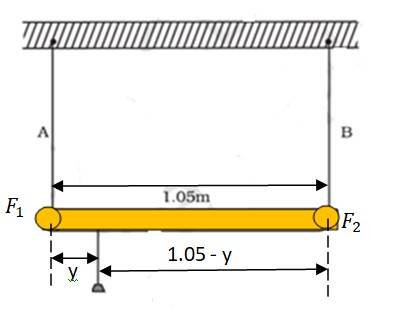
If the two wires have equal stresses, then
= or = = ………(i)
Where is the force exerted on steel wire and is the force exerted on aluminium wire
Taking a moment around the point of suspension, we get
=
= ……(ii)
Using equation (i) and (ii), we can
New answer posted
8 months agoContributor-Level 10
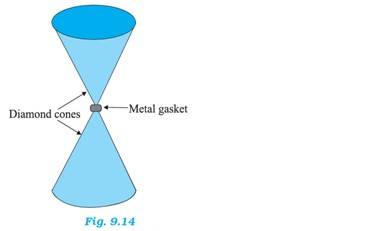
Diameter of the cone at the narrow end, d = 0.5 mm = 0.5 m
Radius, r = d/2 = 0.25 m
Area, A = = 1.96
Compressional force, F = 50000 N
Pressure at the tip of the anvil, p = F/A = 50000/1.96 Pa = 2.54 Pa
New answer posted
8 months agoContributor-Level 10
Volume of water, V = 1 liter. If the water is compressed by 10%, then
ΔV = 0.10% of V= (0.1/100) = 1
Bulk modulus of water, k = 2.2 N/
From the relation, k = , we get ΔP = k = 2.2 1 = 2.2 N/
New answer posted
8 months agoContributor-Level 10
Length of an edge of the solid copper cube, l = 10 cm = 0.1 m
Volume of the copper cube = 1
Hydraulic pressure, p = 7.0 Pa
Bulk modulus of copper, k = 140 Pa
From the relation k = we get = = = 5
New answer posted
8 months agoContributor-Level 10
Hydraulic pressure exerted on glass slab, p = 10 atm = 10 Pa
Bulk modulus of glass, k = 37 N
From the relation k = , we get = = = 2.976
New answer posted
8 months agoContributor-Level 10
Let us assume the depth = h, pressure at depth, = 80 atm = 80 Pa
Density of water at the surface, = 1.03 kg/
Let density of water at depth h be
Let be the volume at the surface and be the volume at depth h and ΔV be the change in volume. Let m be the mass of water.
ΔV = From the relation m = we get
ΔV = m ( - ) = ( - )
= 1- ……(i)
Bulk modulus of water, k = =
= …….(ii)
Bulk modulus of water, k = 2.1 Pa
Hence = 3
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers