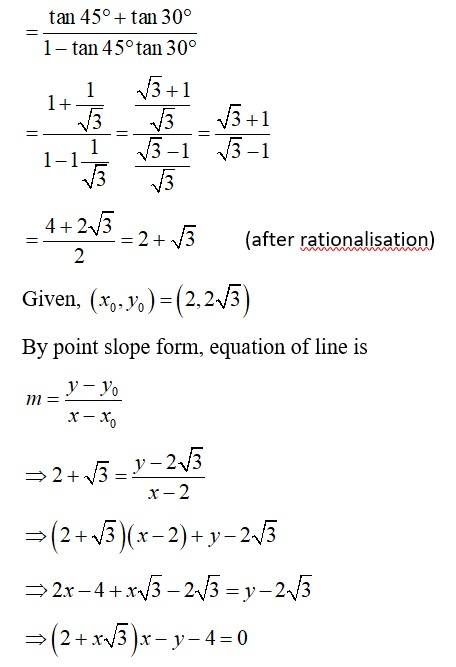Class 11th
Get insights from 8k questions on Class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
8 months agoContributor-Level 10
25.
Let P(1, 0) and Q(2, 3) be the given points. Then, slope of line joining PQ,
If A divides PQ with ratio 1:n, co-ordinate of A is
So, slope of line perpendicular to line joining points P and Q
Hence, equation of line passing through point A and (perpendicular to line) joining points P and Q is given by
New answer posted
8 months agoContributor-Level 10
24.
Slope of line passing through points (2, 5) and (–3, 6) is
So, slope of line perpendicular to line through (2, 5) and (–3, 6) is
Equation of line with slope 5 and passing through (–3, 5) is
New answer posted
8 months agoContributor-Level 10
23.
Let RM be the median draw from vertex R so that M is the mid-point of line segment PQ. Then,
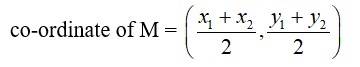
= (0, 2)
So equation of line passing through R (4, 5) and M (0, 2) is
New answer posted
8 months agoContributor-Level 10
23.
Given P = 5 and W = 30°
Using normal form, equation of line is
x cos W + y sin W = P
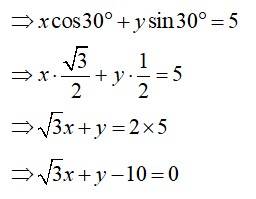
New answer posted
8 months agoContributor-Level 10
21
.Here (x1, y1) = (–1, 1) and (x2, y2) = (2, –4)
Using two point form, equation of line is
New answer posted
8 months agoContributor-Level 10
20.
The slope of the line is m = tan 30° =
And x-intercept, c = 2
Using slope intercept form, equation of line is
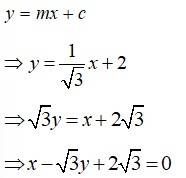
New answer posted
8 months agoContributor-Level 10
19.
Given m = –2
x-intercept, d = –3
Using slope intercept form, equation of line is
y = m (x – d)
New answer posted
8 months agoNew answer posted
8 months agoContributor-Level 10
17.
Given slope = m and
By point slope from, equation of line is
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 684k Reviews
- 1800k Answers