Class 11th

5. Find the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points P (0, – 4) and B (8, 0).

0 Follower 6 Views

Contributor-Level 10

Let 0 (0, 0) be the origin and A be the mid-point of line joining P (0, –4) and B (8, 0)

Then, co-ordinate of A = $(\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2}) = (\frac{0 + 8}{2}, \frac{- 4 + 0}{2}) = (4, - 2)$

$∴$ Slope of OA, m = $\frac{y_{2} - y_{1}}{x_{2} - x_{1}} = \frac{- 2 - 0}{4 - 0} = - \frac{2}{4} = \frac{- 1}{2}$

0 0

New answer posted

8 months ago

4. Find a point on the x-axis, which is equidistant from the points (7, 6) and (3, 4).

0 Follower 8 Views

Contributor-Level 10

Let A (x, 0) be the point on x-axis when is equidistant from P (7, 6) and Q (3, 4)

Then, PA = QA

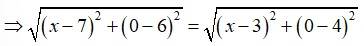
Squaring both sides, we get,

$\Rightarrow x^{2} - 14 x + 49 + 36 = x^{2} - 6 x + 9 + 16$

$\Rightarrow 49 + 36 - 9 - 16 = 14 x - 6 x$

$\Rightarrow 60 = 8 x$

$\Rightarrow x = \frac{60}{8} = \frac{15}{2}$

$∴$ The required point on x-axis is $(\frac{15}{2}, 0) .$

0 0

New answer posted

8 months ago

3. Find the distance between P (x1, y1) and Q (x2, y2) when : (i) PQ is parallel to the y-axis, (ii) PQ is parallel to the x-axis.

0 Follower 13 Views

Contributor-Level 10

0 0

New question posted

8 months ago

3. Find the distance between P (x1, y1) and Q (x2, y2) when : (i) PQ is parallel to the y-axis, (ii) PQ is parallel to the x-axis.

0 Follower 11 Views

New answer posted

8 months ago

2. The base of an equilateral triangle with side 2a lies along the y-axis such that the mid-point of the base is at the origin. Find vertices of the triangle.

0 Follower 45 Views

Contributor-Level 10

2. Let ABC be the equilateral triangle of side 2a and 0 be the origin. Then

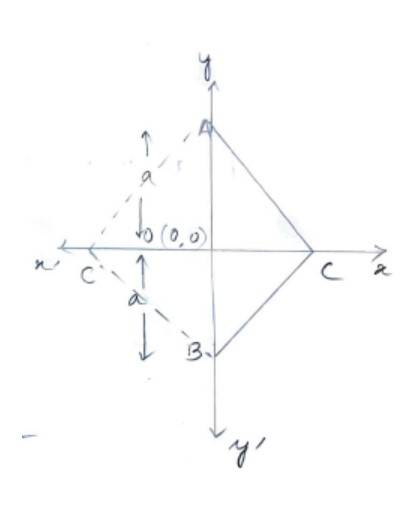
AB = BC = AC = 2a

O is the mid-point of AB we have AO = a

BO = a

We know that A and B lies on y-axis so they have co-ordinate of the form (0, y).

Hence, co-ordinate of A is (0, a) and that of B is (0, –a)

Since OC, bisects AB at right angle, by Pythagoras theorem,

AC²= OA² + OC²

$\Rightarrow {(2 a)}^{2} = {(a)}^{2} +OC^{2}$

$\RightarrowOC^{2} = 4 a^{2} - a^{2}$

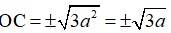
And as C we on x-axis it has co-ordinate of the form (x, 0)

0 0

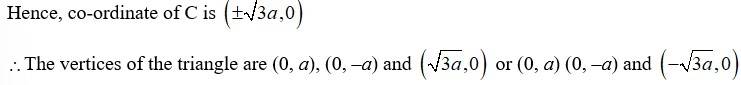
New answer posted

8 months ago

Q1. Draw a quadrilateral in the Cartesian plane, whose vertices are (– 4, 5), (0, 7), (5, – 5) and (– 4, –2). Also, find its area.

0 Follower 76 Views

Contributor-Level 10

Exercise 9.1

1. Let the given points be A(–4, 5), B(0, 7), C(5, –5) and D(–4, –2).

Then quadrilated ABCD can be plotted on the graph by joining the points A, B, C and D.

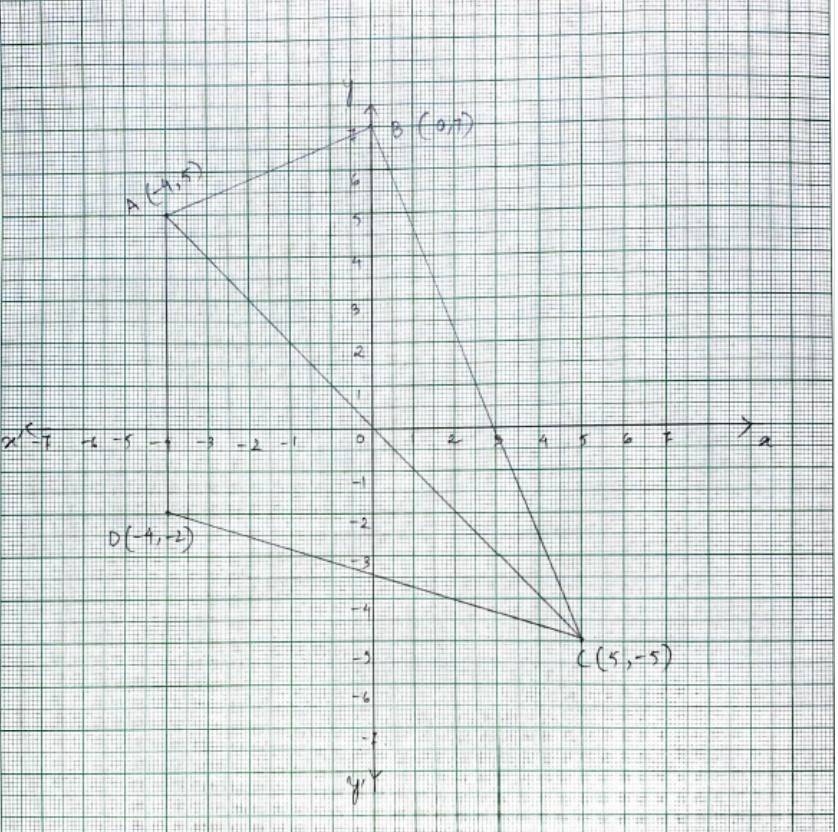
We connect diagonal AC such that

area (ABCD) = (ΔABC) + (ΔADC)

Now,

$(ΔABC) = \frac{1}{2} | x_{1} (y_{2} - y_{3}) + x_{2} (y_{3} - y_{1}) + x_{3} (y_{1} - y_{2}) |$

$= \frac{1}{2} | - 4 [7 - (- 5)] + 0 [- 5 - 5] + 5 [5 - 7] | unit^{2}$

$= \frac{1}{2} | - 4 (7 + 5) + 0 + 5 (5 - 7) | unit^{2}$

$= \frac{1}{2} | (- 4) * 12 + 5 * (- 2) |unit^{2}$

$= \frac{1}{2} | - 48 - 10 |unit^{2}$

$= \frac{1}{2} | - 58 | unit^{2}$

$= \frac{58}{2} unit^{2} = 29 unit^{2}$

Similarly, $(ΔACD) = \frac{1}{2} | x_{1} (y_{2} - y_{3}) + x_{2} (y_{3} - y_{1}) + x_{3} (y_{1} - y_{2}) |$

$= \frac{1}{2} | - 4 [- 5 - (2)] + 5 [- 2 - 5] + (- 4) [5 - (- 5)] | unit^{2}$

$= \frac{1}{2} | - 4 (- 5 + 2) + 5 (- 2 - 5) - 4 (5 + 5) |unit^{2}$

$= \frac{1}{2} | (- 4) * (- 3) + 5 * (- 7) - 4 * (10) |unit^{2}$

$= \frac{1}{2} | 12 - 35 - 40 |unit^{2}$

$= \frac{1}{2} | - 63 | unit^{2}$

$= \frac{63}{2} unit^{2}$

Hence, area (ABCD) = $29 + \frac{63}{2} unit^{2}$

$= \frac{58 + 63}{2} unit^{2} = \frac{121}{2} unit^{2}$

0 0

New answer posted

8 months ago

10.31 (a) It is known that density $ρ$ of air decreases with height y as

where $ρ = ρ_{o} e^{\frac{- y}{y_{o}}}$ = 1.25 kg m^–3 is the density at sea level, and $ρ_{o}$ is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant.

(b) A large He balloon of volume 1425 m3 is used to lift a payload of 400 kg. Assume that the balloon maintains constant radius as it rises. How high does it rise?

[Take $y_{o}$ = 8000 m and $y_{o}$ = 0.18 kg m–3].

0 Follower 4 Views

Contributor-Level 10

Volume of the balloon, V = 1425 $ρ_{H e}$

Mass of the payload, m = 400 kg

Acceleration due to gravity, g = 9.8 m/ $m^{3}$

$s^{2}$ = 8000 m

$y_{o}$ = 0.18 kg m^–3

$ρ_{H e}$ = 1.25 kg m^–3

Density of the balloon = $ρ_{o}$

Height to which the balloon will rise = y

Density of air decreases with height and the relationship is given by:

$ρ$ = $ρ = ρ_{o} e^{\frac{- y}{y_{o}}}$ ……(i)

Differentiating equation (i), we get

$\frac{ρ}{ρ_{o}}$ $e^{\frac{- y}{y_{o}}}$

$- \frac{d ρ}{d y}$ , where k is the constant of proportionality

$α ρ$ , height changes from 0 to y, while density changes from $\frac{d ρ}{d y} = - k ρ$ to $\frac{d ρ}{ρ} = - k d y$ . Integrating both sides between the limits, we get:

$ρ_{o}$

$ρ$ = -ky

$\int_{ρ_{o}}^{ρ} \frac{d ρ}{ρ} = - \int_{0}^{y} k d y$ = ${[\log_{e} ? ρ]}_{ρ_{o}}^{ρ}$ ….(ii)

From equation (i) and (ii), we get

$\frac{ρ}{ρ_{o}}$ =&nbs

...more

Volume of the balloon, V = 1425 $ρ_{H e}$

Mass of the payload, m = 400 kg

Acceleration due to gravity, g = 9.8 m/ $m^{3}$

$s^{2}$ = 8000 m

$y_{o}$ = 0.18 kg m^–3

$ρ_{H e}$ = 1.25 kg m^–3

Density of the balloon = $ρ_{o}$

Height to which the balloon will rise = y

Density of air decreases with height and the relationship is given by:

$ρ$ = $ρ = ρ_{o} e^{\frac{- y}{y_{o}}}$ ……(i)

Differentiating equation (i), we get

$\frac{ρ}{ρ_{o}}$ $e^{\frac{- y}{y_{o}}}$

$- \frac{d ρ}{d y}$ , where k is the constant of proportionality

$α ρ$ , height changes from 0 to y, while density changes from $\frac{d ρ}{d y} = - k ρ$ to $\frac{d ρ}{ρ} = - k d y$ . Integrating both sides between the limits, we get:

$ρ_{o}$

$ρ$ = -ky

$\int_{ρ_{o}}^{ρ} \frac{d ρ}{ρ} = - \int_{0}^{y} k d y$ = ${[\log_{e} ? ρ]}_{ρ_{o}}^{ρ}$ ….(ii)

From equation (i) and (ii), we get

$\frac{ρ}{ρ_{o}}$ = $e^{- k y}$ , k = $y_{0}$

Substituting the value of k in equation (ii), we get

$\frac{1}{k}$

Density $\frac{1}{y_{o}}$ = $ρ = ρ_{o} e^{\frac{- y}{y_{o}}} \dots \dots (i i i)$

= $ρ = \frac{M a s s}{V o l u m e} = \frac{M a s s o f t h e p a y l o a d + M a s s o f h e l i u m}{V o l u m e}$ = 0.461 kg/ $\frac{m + V ρ_{H e}}{V}$

From equation (iii), taking log on both sides

$\frac{400 + 1425 * 0.18}{1425}$ = - $m^{3}$

y = -8000 $\log_{e} ? \frac{ρ}{ρ_{o}}$ = 8000 m = 8 km

The balloon will rise to 8 km

less

0 0

New answer posted

8 months ago

10.30 Two narrow bores of diameters 3.0 mm and 6.0 mm are joined together to form a U-tube open at both ends. If the U-tube contains water, what is the difference in its levels in the two limbs of the tube? Surface tension of water at the temperature of the experiment is 7.3 * 10^–2 N m–1. Take the angle of contact to be zero and density of water to be 1.0 * 103 kg m^–3 (g = 9.8 m s^–2)

0 Follower 2 Views

Contributor-Level 10

Diameter of the 1st bore, $d_{1}$ = 3 mm = 3 $* 10^{- 3}$ m

Radius of the first bore, $r_{1}$ = 1.5 mm = 1.5 $* 10^{- 3}$ m

Diameter of the 2nd bore, $d_{2}$ = 6 mm = 6 $* 10^{- 3}$ m

Radius of the 2nd bore, $r_{2}$ = 3.0 mm = 3 $* 10^{- 3}$ m

Surface tension of water, s= 7.3 $* 10^{- 2}$ N/m

Angle of contact between the bore surface and water, $θ = 0$

Density of water, $ρ = 1.0 * 10^{3}$ kg/ $m^{3}$

Acceleration due to gravity. g = 9.8 m/ $s^{2}$

Let $h_{1}$ and $h_{2}$ be the heights to which water rises in 1st and 2nd tubes respectively. These heights are given by the relations:

$h_{1} = {(2 s c o s ? θ) / ρ g r}_{1}$ …(i)

$h_{2} = {(2 s c o s ? θ) / ρ g r}_{2}$ …(ii)

The difference in level of water in the 2 li

...more

Diameter of the 1st bore, $d_{1}$ = 3 mm = 3 $* 10^{- 3}$ m

Radius of the first bore, $r_{1}$ = 1.5 mm = 1.5 $* 10^{- 3}$ m

Diameter of the 2nd bore, $d_{2}$ = 6 mm = 6 $* 10^{- 3}$ m

Radius of the 2nd bore, $r_{2}$ = 3.0 mm = 3 $* 10^{- 3}$ m

Surface tension of water, s= 7.3 $* 10^{- 2}$ N/m

Angle of contact between the bore surface and water, $θ = 0$

Density of water, $ρ = 1.0 * 10^{3}$ kg/ $m^{3}$

Acceleration due to gravity. g = 9.8 m/ $s^{2}$

Let $h_{1}$ and $h_{2}$ be the heights to which water rises in 1st and 2nd tubes respectively. These heights are given by the relations:

$h_{1} = {(2 s c o s ? θ) / ρ g r}_{1}$ …(i)

$h_{2} = {(2 s c o s ? θ) / ρ g r}_{2}$ …(ii)

The difference in level of water in the 2 limbs

$h_{1} - h_{2}$ = $\frac{2 s c o s ? θ}{ρ g}$ ( $\frac{1}{r_{1}}$ - $\frac{1}{r_{2}})$

= $\frac{2 * 7.3 * 10^{- 2} * c o s ? 0}{1.0 * 10^{3} * 9.8}$ ( $\frac{1}{1.5 * 10^{- 3}}$ - $\frac{1}{3 * 10^{- 3}})$ = 4.965 $* 10^{- 3}$ m = 4.965 mm

less

0 0

New answer posted

8 months ago

10.29 Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 0.465 N m^–1. Density of mercury = 13.6 * 10³kg m^–3.

0 Follower 2 Views

Contributor-Level 10

Radius of the narrow tube, r = 1 mm= 1 $* 10^{- 3}$ m

Surface tension of mercury at the given temperature, s= 0.465 N/m

Density of mercury $ρ = 13.6 * 10^{3}$ kg/ $m^{3}$

Dipping depth = h

Acceleration due to gravity, g = 9.8 m/ $s^{2}$

Surface tension related with angle of contact and dipping depth is given by:

s = $\frac{h ρ g r}{2 \cos ? θ}$ or h = $\frac{2 scos ? θ}{ρ g r}$ = $\frac{2 * 0.465 * \cos ? 140 °}{13.6 * 10^{3} * 9.8 * 1 * 10^{- 3}}$ = -5.345 $* 10^{- 3}$ m= -5.345 mm

0 0

New answer posted

8 months ago

10.28 In Millikan's oil drop experiment, what is the terminal speed of an uncharged drop of radius 2.0 * 10^–5 m and density 1.2 * 10³ kg m^–3. Take the viscosity of air at the temperature of the experiment to be 1.8 * 10^–5 Pa s. How much is the viscous force on the drop at that speed ? Neglect buoyancy of the drop due to air.

0 Follower 2 Views