Class 12th
Get insights from 11.8k questions on Class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
8 months agoContributor-Level 10
The line passes through the point with position vector,
The given vector:
The line which passes through a point with position vector and parallel to is given by,
This is required equation of the line in vector form.
Now,
Let
Comparing the coefficient to eliminate ,
New answer posted
8 months agoContributor-Level 10
28. Given, f (x)
For continuity at x = 5,
f (5) = 5k + 1
So,
i e, 5k + 1 = 10
5k = 10 1
k =
New answer posted
8 months agoContributor-Level 10
Given,
The line passes through the point .
Position vector of A,
Let
The line which passes through point and parallel to is given by,
, where is constant
New answer posted
8 months agoContributor-Level 10
Let AB be the line through the point and and CD be line through the point and
Direction cosine, of AB are
Direction cosine, of CD are
AB will be parallel to CD only
If
Here,
Therefore, AB is parallel to CD.
New answer posted
8 months agoContributor-Level 10
Let AB be the line joining the points and and CD be the line joining the point and .
The direction ratios, a, b, c of AB are
The direction ratios of CD are
AB and CD will be perpendicular to each other, if
Therefore, AB and CD are perpendicular to each other.
New answer posted
8 months agoContributor-Level 10
Two lines with direction cosines l, m, n and l2, m2, n2 are perpendicular to each other, if .
Now, for the 3 lines with direction cosine,
Hence, the lines are perpendicular.
For lines with direction cosines,
Hence, these lines are perpendicular.
For the lines with direction cosines,
Hence, these lines are perpendicular.
Therefore, all the lines are perpendicular.
New answer posted
8 months agoContributor-Level 10
The vertices of ABC are A (3,5, -4), B (-1,1,2) and C (-5, -5, -2)
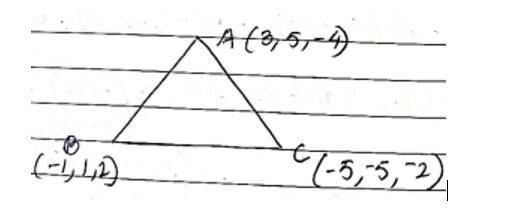
Direction cosine of AB,
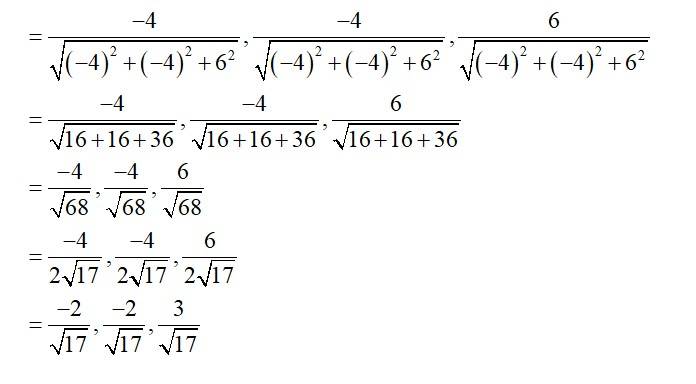
Direction ratios of BC=
Direction cosine of BC = 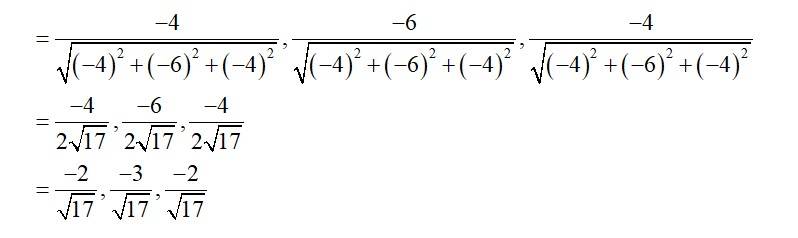
Direction of CA=
Direction cosine of CA = 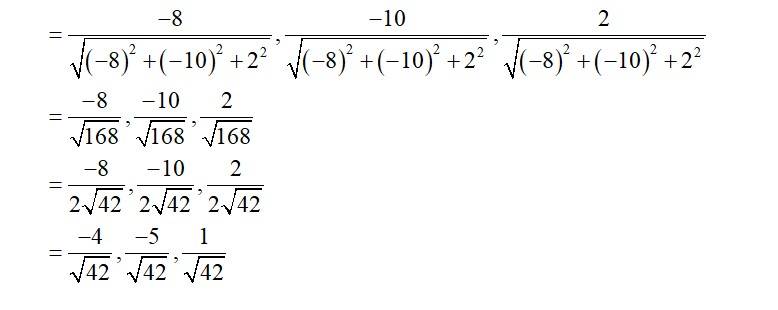
New answer posted
8 months agoContributor-Level 10
Given,
A (2,3,4), B (-1, -2,1), C (5,8,7)
Direction ratio of AB=
Where, a1=3, b1=-5, c1=-3
Direction ratio of BC=
Where, a2=6, b2=10, c2=6
Now,
Here, direction ratio of two-line segments are proportional.
So, A, B, C are collinear.
New answer posted
8 months agoContributor-Level 10
26. Given f (x) =
For continuous at x = 2,
f (2) = k (2)2 = 4x.
L.H.L. =
R.H.L. =
Then, L.H.L = R.H.L. = f (2)
i e, 4x = 3
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 685k Reviews
- 1800k Answers
