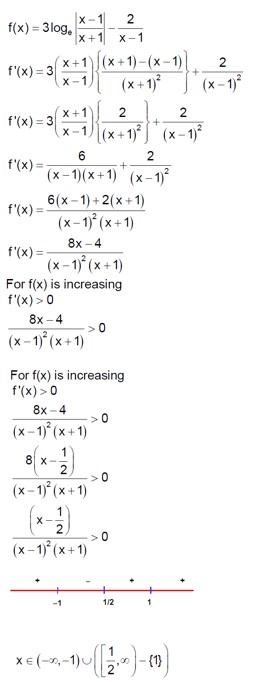Class 12th
Get insights from 12k questions on Class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
4 months agoContributor-Level 9
m = 10 molal
K_b = 0.5 K kg mol? ¹
Using: ΔT_b = I K_b m
and α = (i - 1) / (n - 1)
n for AB? is 3; α = 0.1
0.1 = (i - 1) / (3 - 1) ⇒ I = 1.2
ΔT_b = 1.2 * 0.5 * 10 = 6 °C
So, boiling point of solution = 100 + 6 = 106 °C
New answer posted
4 months agoContributor-Level 9
A 6.5 molal solution means 6.5 moles of KOH is in 1 kg (1000 g) of solvent (H? O).
Moles of solute, n_B = 6.5
Mass of solute, W_B = 6.5 * 56 = 364 g
Mass of solvent, W_A = 1000 g
Mass of solution = 1364 g
Volume of solution = 1364 / 1.89 mL
Now, molarity = [6.5 / (1364 / 1.89)] * 1000 M = 9 M
New answer posted
4 months agoContributor-Level 9
Solubility product of A? X = 4S? ³
Where S? is the solubility of salt A? X.
Solubility product of MX = S? ²
Where S? is the solubility of MX.
Given 4S? ³ = 4 * 10? ¹² ⇒ S? = 10? M
Given S? ² = 4 * 10? ¹² ⇒ S? = 2 * 10? M
So, S? / S? = 10? / (2 * 10? ) = 50
New answer posted
4 months agoContributor-Level 10
Solve sin? ¹ (3x/5) + sin? ¹ (4x/5) = sin? ¹x.
Using the formula sin? ¹a + sin? ¹b = sin? ¹ (a√ (1-b²) + b√ (1-a²):
sin? ¹ ( (3x/5)√ (1 - (4x/5)²) + (4x/5)√ (1 - (3x/5)²) ) = sin? ¹x
(3x/5) * √ (1 - 16x²/25) + (4x/5) * √ (1 - 9x²/25) = x
x * [ (3/5) * √ (25-16x²)/5 + (4/5) * √ (25-9x²)/5 - 1 ] = 0
So, x = 0 is one solution.
For the other part:
3√ (25-16x²) + 4√ (25-9x²) = 25
Let's check integer solutions. If x = 1:
3√ (9) + 4√ (16) = 33 + 44 = 9 + 16 = 25. So x = 1 is a solution.
If x = -1:
3√ (9) + 4√ (16) = 25. So x = -1 is a solution.
The solutions are x = 0, 1, -1.
New answer posted
4 months agoContributor-Level 9
Edge length in bcc, a? = 27 Å
Let, Edge length in fcc be a? Å
Now, the same element crystallises in bcc as well as fcc.
For bcc: 4r = √3 a? ⇒ r = (√3 / 4) a?
For fcc: 4r = √2 a? ⇒ r = a? / (2√2)
So, (√3 / 4) a? = a? / (2√2)
(√3 / 4) * 27 = a? / (2√2)
a? = 33.13 Å
The nearest integer is 33.
New answer posted
4 months agoContributor-Level 9
Roasting is a process in which sulphur is removed as SO? gas from sulphide ores on heating in excess of oxygen.
New answer posted
4 months agoContributor-Level 9
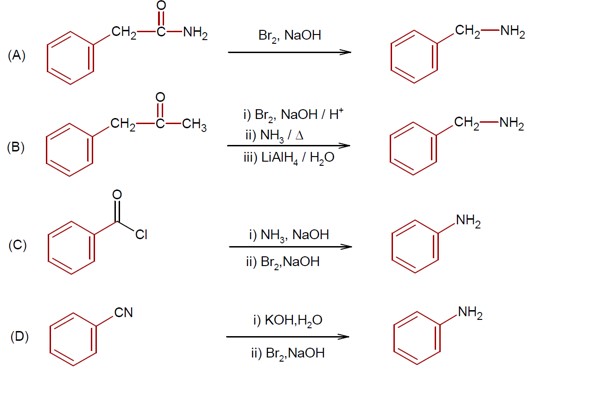
R-CONH? + Br? + 4NaOH → R-NH? + 2NaBr + Na? CO? + 2H? O
This reaction is the Hoffmann bromamide degradation, in which an amide is converted to a 1° amine.
New answer posted
4 months agoContributor-Level 10
The shortest distance D between two skew lines is given by the formula:
D = | (a? - a? ) ⋅ (b? x b? )| / |b? x b? |
Line L? : (x-1)/2 = (y-2)/3 = (z-4)/4
Line L? : (x-2)/3 = (y-4)/4 = (z-5)/5
Here, a? = I + 2j + 4k, b? = 2i + 3j + 4k
a? = 2i + 4j + 5k, b? = 3i + 4j + 5k
a? - a? = I + 2j + k
b? x b? = | I j k |
| 2 3 4 |
| 3 4 5 |
= I (15-16) - j (10-12) + k (8-9) = -i + 2j - k
D = | (i + 2j + k) ⋅ (-i + 2j - k)| / √ (-1)² + 2² + (-1)²)
= |-1 + 4 - 1| / √ (1 + 4 + 1)
= 2 / √6
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers