Class 12th
Get insights from 11.9k questions on Class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
Given the refractive index μ = λ? / λ = 3/2 and v = 10m, the object distance is u = - (3/2)v = -15m.
Using the lens maker's formula:
μ/v - 1/u = (μ - 1)/R
(3/2)/10 - 1/ (-15) = (3/2 - 1)/R
This gives the radius of curvature R:
R = -30/13 m
New answer posted
7 months agoContributor-Level 9
Resonance frequency is independent of R.
Quality factor = ωL/R ⇒ Quality factor decreases with increase in R.
Bandwidth of resonance circuit = R/L ⇒ increases with increase in R.
New answer posted
7 months ago
Contributor-Level 10
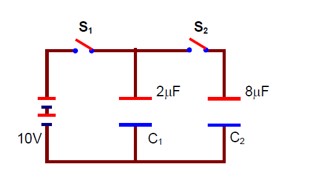
Let the charge on C? be q µC. For the capacitor network:
q/C? = (C? * 10 - q) / C? ⇒ q/8 = (2 * 10 - q) / 2 ⇒ q = 16
New answer posted
7 months agoContributor-Level 9
λ? /λ? = (m? v? ) / (m? v? ) ⇒ m? = m? (v? /v? ) (λ? /λ? ) = m? (1/4) (1/2) = (1/8)m?
New answer posted
7 months agoContributor-Level 10
The system of equations has no solution if the determinant of the coefficient matrix is zero.
Δ = |k 1|
|1 k 1|
|1 k|
Δ = k (k² - 1) - 1 (k - 1) + 1 (1 - k) = 0
Δ = k³ - k - k + 1 + 1 - k = 0
⇒ k³ - 3k + 2 = 0 ⇒ (k - 1)² (k + 2) = 0
∴ k = -2, 1
If k = 1 then all the equations are identical (infinite solutions). Hence k = -2 for no solution.
New answer posted
7 months ago
Contributor-Level 10
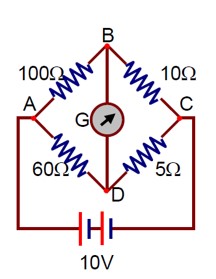
Let V? = 10V, V? = xV, V? = 0V, and V? = yV.
Applying Kirchhoff's current law at node B:
(x - 10)/100 + (x - y)/15 + (x - 0)/10 = 0 ⇒ 53x - 20y = 30 . (1)
Applying Kirchhoff's current law at node D:
(y - 10)/60 + (y - x)/15 + (y - 0)/5 = 0 ⇒ 17y - 4x = 10 . (2)
Solving equations (1) and (2), we get:
x = 0.865 and y = 0.792
The current i? is:
i? = (x - y) / 15 = 4.87 mA
New answer posted
7 months agoContributor-Level 10
dy/dx = xy - 1 + x - y = x (y + 1) - (y + 1) = (x - 1) (y + 1)
⇒ ∫ dy / (1 + y) = ∫ (x - 1) dx ⇒ ln (1 + y) = x²/2 - x + C
For y (0) = 0, c = 0. ∴ ln (1 + y) = x²/2 - x
1 + y = e^ (x²/2 - x)
y (1) = e^ (1/2 - 1) - 1 = e^ (-1/2) - 1
New answer posted
7 months agoContributor-Level 9
In external magnetic field, a magnetic force acts on every small part of the loop in direction perpendicular to the wire. Thus, loop assumes a shape (circular) in which it covers maximum area
New answer posted
7 months agoContributor-Level 10
The Balmer series lies in the visible region of the electromagnetic spectrum.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 687k Reviews
- 1800k Answers