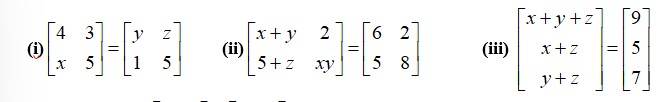Class 12th
Get insights from 11.8k questions on Class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
8 months agoContributor-Level 10
(i)
corresponding
By equating the elements of the matrices, we get,
x= 1
y= 4
z= 3.
(ii)
By equating the corresponding elements of the matrices we get,
x+ y = 6 (I)
5 + Z = 5
xy = 8
x
putting eq in (1) we get
+ y = 6.
8 + y2 = 6y
y2 6y + 8 = 0.
y2 - 4y - 2y + 8 = 0
y (y-4) -2 (y-4) = 0
(y-4) (y-2) = 0
y= 4 0r y = 2.
When y = 4,x= 6-y = 6-4 = and z = 0.
Wheny = 2,x = 6-y = 6-2 = 4 and z = 0.
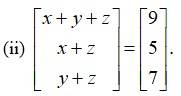
By equating the corresponding elements of the matrices we get,
x+ y + z = 9 -------(i)
x + z = 7 --------(ii)
y + z = 7 -------(iii)
Subtracting eqn (3) from (1) and (2) from (1) we get,
x + y + z -y - z = 9 - 7 and x
New answer posted
8 months agoContributor-Level 10
(E) (i) aij = such that i = 1, 2, 3 and j = 1, 2, 3, 4 for 3 * 4 matrix
So, a11= .
a12 =
a14 =
a21 =
a22 =
a23 =

New answer posted
8 months agoContributor-Level 10
(E) (i) aij such that i = 1, 2 and j = 1 * 2 for 2 * 2 matrix
Therefore a11 = A 2*2 =
a12 =
a21
a22 =
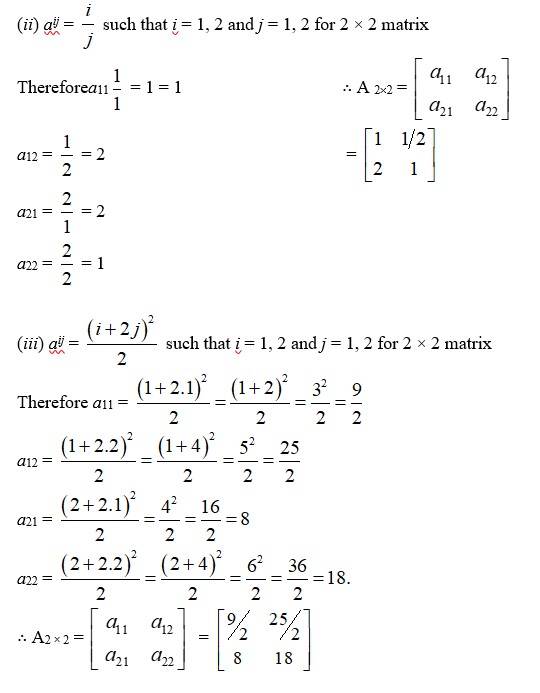
New answer posted
8 months ago3.If a matrix has 18 elements, what are the possible orders it can have? What, if it has 5 elements?
Contributor-Level 10
As number of elements of matrix with order m * n
(E) Possible order of matrix with 18 elements are (1 * 18), (2 * 9), (3 * 6), (6 * 3), (9 * 2) and (18 * 1)
Similarly, possible order of matrix with 5 elements are (1 * 5) and (5 * 1)
New answer posted
8 months agoContributor-Level 10
As, number of elements of matrix having order m * n = m.n.
(b) So, (possible) order of matrix with 24 elements are (1 * 24), (2 * 12), (3 * 8), (4 * 6), (6 * 4), (8 * 3), (12 * 2), 24 * 1).
Similarly, possible order of matrix with 13 elements are (1 * 13) and (13 * 1)
New question posted
8 months agoNew question posted
8 months agoTaking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 684k Reviews
- 1800k Answers