Maths NCERT Exemplar Solutions Class 12th Chapter Three

$\left(\begin{array}{cc}\hfill 1+i\hfill & \hfill 1\hfill \\ \hfill -i\hfill & \hfill 0\hfill \end{array}\right)$

$A^2=\left(\begin{array}{cc}\hfill 1+i\hfill & \hfill 1\hfill \\ \hfill -i\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{cc}\hfill 1+i\hfill & \hfill 1\hfill \\ \hfill -i\hfill & \hfill 0\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill i\hfill & \hfill 1+i\hfill \\ \hfill 1-i\hfill & \hfill -i\hfill \end{array}\right)$

$A^4=\left(\begin{array}{cc}\hfill i\hfill & \hfill 1+i\hfill \\ \hfill 1-i\hfill & \hfill -i\hfill \end{array}\right)\left(\begin{array}{cc}\hfill i\hfill & \hfill 1+i\hfill \\ \hfill 1-i\hfill & \hfill -i\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$

$\therefore A^5=A$

A⁹ = A

$\therefore forn=1,5,9,.....,97$

total possible values of n = 25

$\begin{array}{cc}\hfill 2x-3y=\gamma +5\hfill & \hfill \alpha x+5y=\left(\beta +1\right)\hfill \end{array}\}infinitelymanysolution$

$\therefore \frac{2}{\alpha }=\frac{-3}{5}=\left(\frac{\gamma +5}{\beta +1}\right)$

(i) $\frac{2}{\alpha }=\frac{-3}{5}=\frac{\gamma +5}{\beta +1}$

$\alpha =\frac{5*2}{-3}$ 5x + 25 = -3β - 3

^{$5\gamma +3\beta =-28$}

^{$\left|9\alpha +5\gamma +3\beta \right|=\left|9*\frac{-10}{3}-28\right|$}

= ^{$\left|-30-28\right|=58$}

$S_n=\frac{n^2}{1-\frac{1}{{\left(n+1\right)}^2}}=\frac{n{\left(n+1\right)}^2}{\left(n+2\right)}={\left(n+1\right)}^2-2\left(n+1\right)+2-\frac{2}{\left(n+2\right)}$

$\frac{1}{26}+{\displaystyle \sum _{n=1}^{50}\left(S_n+\frac{2}{\left(n+1\right)}-\left(n+1\right)\right)=\frac{1}{26}+{\displaystyle \sum _{n=1}^{50}{\left(n+1\right)}^2}-3\left(n+1\right)+2+2\left(\frac{1}{\left(n+1\right)}-\frac{1}{\left(n+2\right)}\right)}$

$=\frac{1}{26}+45525-3*1325+2*50+2\left(\frac{1}{2}-\frac{1}{52}\right)$

$=\frac{1}{26}+41550+100+1-\frac{1}{26}=41651$

$\underset{x\to 1}{lim}\frac{sin\left(3x^2-4x+1\right)-x^2+1}{2x^3-7x^2+ax+b}=-2$

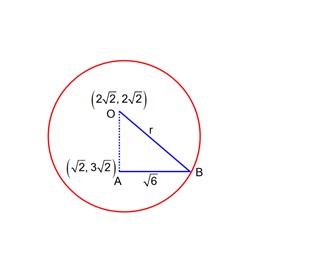
For this limit to be defined 2x³ – 7x² + ax + b should also trend to 0 or x ® 1.

$\therefore 2.{\left(1\right)}^3-7{\left(1\right)}^2+a\cdot 1+b=0$

 2 – 7 + (a + b) = 0

(a + b) = 5 …………….(i)

Now this becomes % form  $\therefore$ we apply L'lopital rule

$\underset{x\to 1}{lim}\frac{\left(3x^2-4x+1\right)-x^2+1}{2x^3-7x^2+ax+b}=\underset{x\to 1}{lim}\frac{cos\left(3x^2-4x+1\right)\left(6x-4\right)-2x}{6x^2-14x+a}$

Now the numerator again ® 0 as x = 1

$\therefore$  6x² – 14x + a ® 0 as x = 1

6 . (1)² – 14 + a = 0

a = 8 …………….(ii)

a + b = 5  $\therefore a-b=8-\left(-3\right)=11$       

(b = -3) ® from (i) & (ii)

  $x^2+y^2-2\sqrt[]{2}x-6\sqrt[]{2}y+14=0$

 centre $\left(\sqrt[]{2},3\sqrt[]{2}\right)$

radius  ${\left({\left(\sqrt[]{2}\right)}^2+{\left(3\sqrt[]{2}\right)}^2-14\right)}^{1/2}$

$={\left(2+18-14\right)}^{1/2}=\left(\sqrt[]{6}\right)$

${\left(x-2\sqrt[]{2}\right)}^2+{\left(y-2\sqrt[]{2}\right)}^2=r^2$

centre  $\left(2\sqrt[]{2},2\sqrt[]{2}\right)$

OA = $\sqrt[]{{\left(2\sqrt[]{2}-\sqrt[]{2}\right)}^2+{\left(2\sqrt[]{2}-3\sqrt[]{2}\right)}^2}=\sqrt[]{2+2}=2$                  

r² = ${\left(\sqrt[]{6}\right)}^2+{\left(2\right)}^2=6+4=10$  

$\frac{1}{7}{\displaystyle \sum _{i=1}^7{\left(x_i-62\right)}^2}=20$ $\overline{x}=62$      

${\displaystyle \sum _{i=1}^7{\left(x_i-62\right)}^2}$ = 140……………… (i)

 If any one student get less 50 marks then   ${\left(x_i-62\right)}^2\ge 144$

but    ${\displaystyle \sum _{i=1}^7{\left(x_i-62\right)}^2}=140$

$\therefore$ both condition cannot satisfy together hence no students fails.

Any point on line L is

M (3r + 6, 2r + 1, 3r + 2)                                                          

$\overrightarrow{PM}\perp rtoL$          

$\therefore 3\left(3r+5\right)+2\left(2r-1\right)+3\left(3r-1\right)=0$          

$r=\frac{-5}{11}$

cota = 1        & secβ =   $\frac{-5}{3}$

< < $\frac{}{}$       $\frac{3\pi }{2}$  secβ =   $\frac{-5}{3}$

$\alpha =\left(\pi +\frac{\pi }{4}\right)$  cosβ = $\frac{-3}{5}=cos\left(180-53\right)$  

tanb =  $\frac{-4}{3}$  

tan(α + β) =   $\frac{tan\alpha +tan\beta }{1-tan\alpha tan\beta }$

$\therefore A-\frac{1}{4}\&4thquadrant.$

$=\frac{1-\frac{4}{3}}{1+\frac{4}{3}}=\frac{-1}{7}$

$\therefore -\frac{1}{4}\&4thquadrant.$

$\underset{n\to \infty }{lim}6tan\left\{{\displaystyle \sum _{r=1}^{n}ta{n}^{-1}}\left(\frac{1}{r^2+3r+3}\right)\right\}$

$=\underset{n\to \infty }{lim}6tan\left\{{\displaystyle \sum _{r=1}^{n}ta{n}^{-1}}\left(\frac{\left(r+2\right)-\left(r+1\right)}{1+\left(r+2\right)\left(r+1\right)}\right)\right\}$

$=\underset{n\to \infty }{lim}6tan\left\{\frac{r}{2}-ta{n}^{-1}\left(2\right)\right\}$

$6*\frac{1}{2}=3$