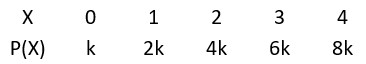- Matrices Long Answers Type Questions
- Matrices Short Answers Type Questions
- Matrices Objective Type Questions
- Matrices Fill in the blanks Type Questions
- Matrices True or False Type Questions
- 24th June 2022 (second shift)
- JEE Mains Solutions 2022,28th june , Maths,Second shift
Matrices Long Answers Type Questions
| Q1. If for any two square matrices, prove by mathematical induction that . |
| Sol.
|
| Q2. Find , , and if: satisfies . |
| Sol. |
Commonly asked questions
If for any two square matrices, prove by mathematical induction that .
This is a Long Answers Type Questions as classified in NCERT Exemplar
Sol.
Find , , and if: satisfies .
This is a Long Answers Type Questions as classified in NCERT Exemplar
Sol.

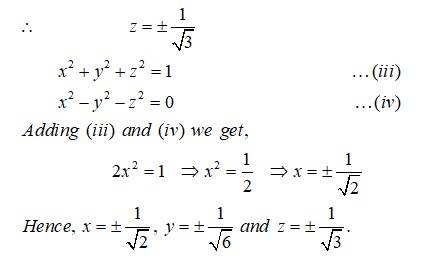
If possible, using elementary row transformations, find the inverse of the following matrices:
(i)
(ii)
(iii)
This is a Long Answers Type Questions as classified in NCERT Exemplar
Sol.
Express the matrix as the sum of a symmetric and a skew-symmetric matrix.
This is a long answer type question as classified in NCERT Exemplar
Matrices Short Answers Type Questions
| Q1. If a matrix has 28 elements, what are the possible orders it can have? What if it has 13 elements? |
| Sol. |
| Q2. In the matrix (i) The order of the matrix . (ii) The number of elements. (iii) Write elements . |
| Sol.
|
Commonly asked questions
If a matrix has 28 elements, what are the possible orders it can have? What if it has 13 elements?
This is a short answer type question as classified in NCERT Exemplar
In the matrix 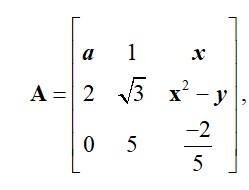 write:
write:
(i) The order of the matrix .
(ii) The number of elements.
(iii) Write elements .
This is a short answer type question as classified in NCERT Exemplar
Construct a2 × 2 matrix where
(i) .
(ii) .
This is a short answer type question as classified in NCERT Exemplar
Construct a matrix whose elements are given by .
This is a short answer type question as classified in NCERT Exemplar
Find values of and if , where
This is a short answer type question as classified in NCERT Exemplar
If possible, find the sum of the matrices and , where
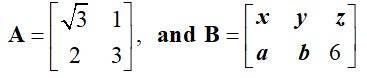
This is a short answer type question as classified in NCERT Exemplar
If 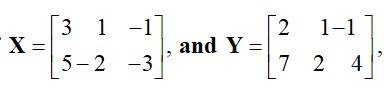 find:
find:
(i) .
(ii) .
(iii) A matrix such that is a zero matrix.
This is a short answer type question as classified in NCERT Exemplar
Find non-zero values of satisfying the matrix equation:
x
This is a short answer type question as classified in NCERT Exemplar
If show that .
This is a short answer type question as classified in NCERT Exemplar
Find the value of if
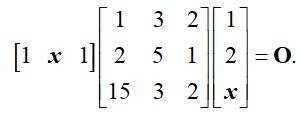
This is a short answer type question as classified in NCERT Exemplar

Show that satisfies the equation , and hence find .
This is a short answer type question as classified in NCERT Exemplar
Find the matrix satisfying the matrix equation:

This is a short answer type question as classified in NCERT Exemplar
Find , if Kindly Consider the following
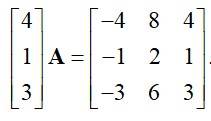
This is a short answer type question as classified in NCERT Exemplar

If 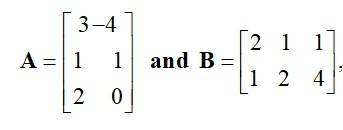 then verify
then verify
This is a short answer type question as classified in NCERT Exemplar

If possible, find and , where 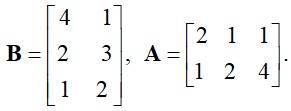
This is a short answer type question as classified in NCERT Exemplar

Show by an example that for , .
This is a short answer type question as classified in NCERT Exemplar
Given  Is ?
Is ?
This is a short answer type question as classified in NCERT Exemplar

Solve for x and y :
Kindly Consider the following
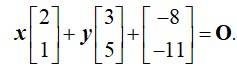
This is a short answer type question as classified in NCERT Exemplar

If X and Y are matrices, then solve the following matrix equations for X and Y:
This is a short answer type question as classified in NCERT Exemplar
If , then find a non-zero matrix such that .
This is a short answer type question as classified in NCERT Exemplar
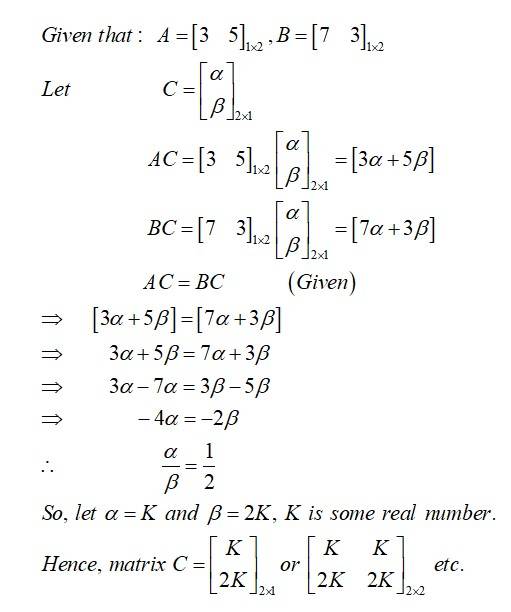
Give an example of matrices , , and such that , where is a non-zero matrix, but .
This is a short answer type question as classified in NCERT Exemplar
If verify:
(i) .
(ii) .
This is a short answer type question as classified in NCERT Exemplar
If prove that .
This is a short answer type question as classified in NCERT Exemplar
Kindly Consider the following 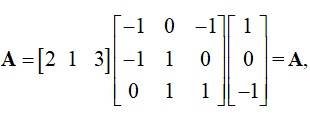 find A.
find A.
This is a short answer type question as classified in NCERT Exemplar

If 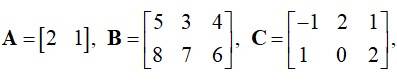 verify that .
verify that .
This is a short answer type question as classified in NCERT Exemplar
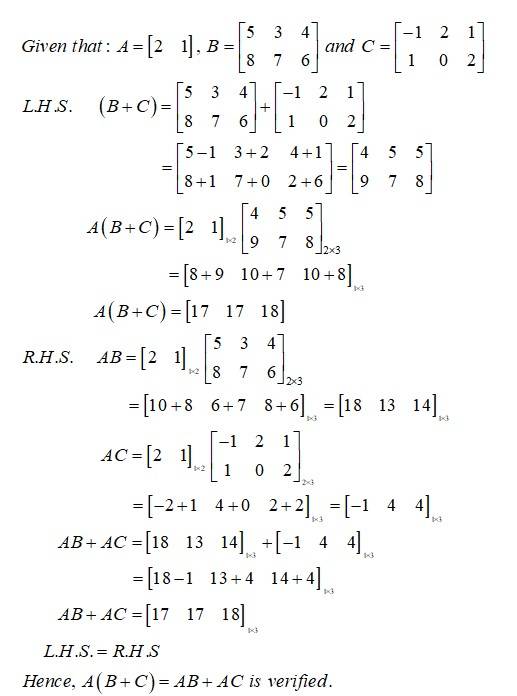
If then verify that , where is a unit matrix.
This is a short answer type question as classified in NCERT Exemplar
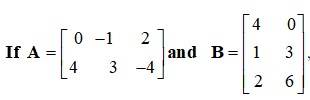 then verify that:
then verify that:
(i) .
(ii) .
(iii) .
This is a short answer type question as classified in NCERT Exemplar


If 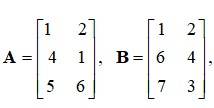 then verify that:
then verify that:
(i) .
(ii) .
This is a short answer type question as classified in NCERT Exemplar


Show that and are both symmetric matrices for any matrix .
This is a short answer type question as classified in NCERT Exemplar
Let and be square matrices of the order . Is ? Give reasons
This is a short answer type question as classified in NCERT Exemplar
Show that if and are square matrices such that , then .
This is a short answer type question as classified in NCERT Exemplar
Let , , , , .
Show that:
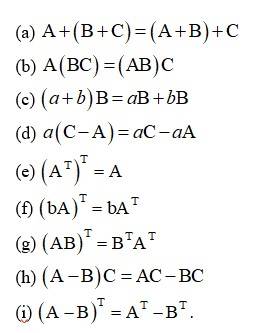
This is a short answer type question as classified in NCERT Exemplar
If , then show that .
This is a short answer type question as classified in NCERT Exemplar
If , , and , then show that .
This is a short answer type question as classified in NCERT Exemplar
Verify that when .
This is a short answer type question as classified in NCERT Exemplar
Prove by Mathematical Induction that , where for any square matrix .
This is a short answer type question as classified in NCERT Exemplar
Find inverse, by elementary row operations (if possible), of the following matrices:
(i)
(ii)
This is a short answer type question as classified in NCERT Exemplar
If , then find the values of , , , and .
This is a short answer type question as classified in NCERT Exemplar
If and , find a matrix such that is a null matrix.
This is a short answer type question as classified in NCERT Exemplar
If , then find . Hence, obtain .
This is a short answer type question as classified in NCERT Exemplar
Find the values of , , , and , if 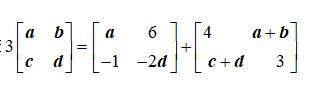
This is a short answer type question as classified in NCERT Exemplar
Find the matrix such that 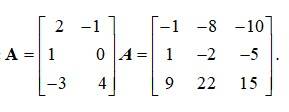
This is a short answer type question as classified in NCERT Exemplar

If , find .
This is a short answer type question as classified in NCERT Exemplar
If , and , find the value of .
This is a short answer type question as classified in NCERT Exemplar
If the matrix is a skew-symmetric matrix, find the values of a, b, and c.
This is a short answer type question as classified in NCERT Exemplar
If , then show that .
This is a short answer type question as classified in NCERT Exemplar

If is a square matrix such that , show that .
This is a short answer type question as classified in NCERT Exemplar
If are square matrices of the same order and is a skew-symmetric matrix, show that is skew-symmetric
This is a short answer type question as classified in NCERT Exemplar
Matrices Objective Type Questions
| Choose the correct answer from the given four options in each of the Exercises 1 to 15: Q1. The matrix is a (A) square matrix (B) diagonal matrix (C) unit matrix (D) none |
| Sol:
|
| Q2. Total number of possible matrices of order
with each entry 2 or 0 is (A) 9 (B) 27 (C) 81 (D) 512 |
| Sol:
|
| Q3. If then the value of is (A) (B) (C) (D) |
| Sol:
|
| Q4. If then is equal to: |
| Sol:
|
| Q5. If and are two matrices of the order and , respectively, and , then the order of the matrix is (A) (B) (C) (D) |
| Sol:
|
| Q6. If , then is equal to (A) (B) (C) (D) |
| Sol:
|
| Q7. If matrix
, where
if
if ,then is equal to (A) I (B) A (C) 0 (D) None of these |
| Sol:
|
| Q8.The matrix
is a (A) Identity matrix (B) Symmetric matrix (C) Skew symmetric matrix (D) None of these |
| Sol:
|
| Q9. The matrix
is a (A) Diagonal matrix (B) Symmetric matrix (C) Skew symmetric matrix (D) Scalar matrix |
| Sol:
|
| Q10. If
is a matrix of order
and
is a matrix such that
and
are both defined, then the order of matrix
is (A) (B) (C) (D) |
| Sol:
|
| Q11. If
and
are matrices of the same order, then
is a (A) Skew symmetric matrix (B) Null matrix (C) Symmetric matrix (D) Unit matrix |
| Sol:
|
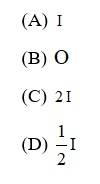
| Q12. If
is a square matrix such that
, then
is equal to (A) A (B) I - A (C) I + A (D) 3A |
| Sol:
|
| Q13. For any two matrices
and
, we have (A) AB = BA (B) AB BA (C) AB = O (D) None of the above |
| Sol:
|
| Q14. On using elementary column operations
in the following matrix equation:
we have: (A) (B) (C) (D) |
| Sol:
|
| Q15. On using elementary row operation
in the following matrix equation: we have: (A) (B) (C) (D) |
| Sol:
|
Commonly asked questions
The matrix is a
(A) Square matrix
(B) Diagonal matrix
(C) Unit matrix
(D) None
This is an Objective Type Questions as classified in NCERT Exemplar
Total number of possible matrices of order with each entry 2 or 0 is
(A) 9
(B) 27
(C) 81
(D) 512
This is an Objective Type Questions as classified in NCERT Exemplar
If then the value of is
(A)
(B)
(C)
(D)
This is an Objective Type Questions as classified in NCERT Exemplar
If then is equal to:
This is an Objective Type Questions as classified in NCERT Exemplar
If and are two matrices of the order and , respectively, and , then the order of the matrix is
(A)
(B)
(C)
(D)
This is an Objective Type Questions as classified in NCERT Exemplar
If , then is equal to
(A)
(B)
(C)
(D)
This is an Objective Type Questions as classified in NCERT Exemplar
If matrix , where if if ,then is equal to
(A) I
(B) A
(C) 0
(D) None of these
This is an Objective Type Questions as classified in NCERT Exemplar
The matrix is a
(A) Identity matrix
(B) Symmetric matrix
(C) Skew symmetric matrix
(D) None of these
This is an Objective Type Questions as classified in NCERT Exemplar
The matrix is a
(A) Diagonal matrix
(B) Symmetric matrix
(C) Skew symmetric matrix
(D) Scalar matrix
This is an Objective Type Questions as classified in NCERT Exemplar
10. If is a matrix of order and is a matrix such that and are both defined, then the order of matrix is
(A)
(B)
(C)
(D)
This is an Objective Type Questions as classified in NCERT Exemplar
If and are matrices of the same order, then is a
(A) Skew symmetric matrix
(B) Null matrix
(C) Symmetric matrix
(D) Unit matrix
This is an Objective Type Questions as classified in NCERT Exemplar
If is a square matrix such that , then is equal to
(A) A
(B) I - A
(C) I + A
(D) 3A
This is an Objective Type Questions as classified in NCERT Exemplar
For any two matrices and , we have
(A) AB = BA
(B) AB BA
(C) AB = O
(D) None of the above
This is an Objective Type Questions as classified in NCERT Exemplar
On using elementary column operations in the following matrix equation: we have:
(A)
(B)
(C)
(D)
This is an Objective Type Questions as classified in NCERT Exemplar
On using elementary row operation in the following matrix equation:
we have:
(A)
(B)
(C)
(D)
This is an Objective Type Questions as classified in NCERT Exemplar
Matrices Fill in the blanks Type Questions
| Q1. ___ matrix is both symmetric and skew symmetric matrix. |
| Sol.
|
| Q2. Sum of two skew symmetric matrices is always ___ matrix. |
| Sol.
|
| Q3. The negative of a matrix is obtained by multiplying it by ___. |
| Sol.
|
| Q4. The product of any matrix by the scalar ___ is the null matrix. |
| Sol.
|
| Q5. A matrix which is not a square matrix is called a ___ matrix. |
| Sol.
|
| Q6. Matrix multiplication is ___ over addition. |
| Sol:
|
| Q7. If is a symmetric matrix, then is a ___ matrix. |
| Sol.
|
| Q8. If is a skew symmetric matrix, then is a ___. |
| Sol.
|
| Q9. If
and
are square matrices of the same order, then (i)
___. |
| Sol.
|
| Q10. If is skew symmetric, then is a ___ (k is any scalar). |
| Sol.
|
| Q11. If
and
are symmetric matrices, then (i) is a ___. (ii) is a ___. |
| Sol.
|
| Q12. If is symmetric matrix, then is ___. |
| Sol.
|
| Q13. If and are symmetric matrices of same order, then is symmetric if and only if ___. |
| Sol.
|
| Q14. In applying one or more row operations while finding by elementary row operations, we obtain all zeros in one or more rows, then ___. |
| Sol.
|
Commonly asked questions
___ matrix is both symmetric and skew symmetric matrix.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
Sum of two skew symmetric matrices is always ___ matrix.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
The negative of a matrix is obtained by multiplying it by ___.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
The product of any matrix by the scalar ___ is the null matrix.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
A matrix which is not a square matrix is called a ___ matrix.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
Matrix multiplication is ___ over addition.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
If is a symmetric matrix, then is a ___ matrix.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
If is a skew symmetric matrix, then is a ___.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
If and are square matrices of the same order, then
(i) ___.
(ii) ___ (k is any scalar).
(iii) ___.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
If is skew symmetric, then is a ___ (k is any scalar).
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
If and are symmetric matrices, then
(i) is a ___.
(ii) is a ___.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
If is symmetric matrix, then is ___.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
If and are symmetric matrices of same order, then is symmetric if and only if ___.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
In applying one or more row operations while finding by elementary row operations, we obtain all zeros in one or more rows, then ___.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
Matrices True or False Type Questions
| Q1. A matrix denotes a number. |
| Sol.
|
| Q2. Matrices of any order can be added. |
| Sol.
|
| Q3. Two matrices are equal if they have the same number of rows and the same number of columns. |
| Sol.
|
| Q4. Matrices of different orders cannot be subtracted |
| Sol.
|
| Q5. Matrix addition is associative as well as commutative. |
| Sol.
|
| Q6. Matrix multiplication is commutative. |
| Sol.
|
| Q7. A square matrix where every element is unity is called an identity matrix. |
| Sol.
|
| Q8. If and are two square matrices of the same order, then . |
| Sol.
|
| Q9. If and are two matrices of the same order, then . |
| Sol.
|
| Q10. If matrix , then or or both and are null matrices. |
| Sol.
|
| Q11. Transpose of a column matrix is a column matrix. |
| Sol. |
| Q12. If and are two square matrices of the same order, then . |
| Sol.
|
| Q13. If each of the three matrices of the same order is symmetric, then their sum is a symmetric matrix. |
| Sol.
|
| Q14. If and are any two matrices of the same order, then . |
| Sol.
|
| Q15. If , where and are not square matrices, then the number of rows in is equal to the number of columns in and the number of columns in is equal to the number of rows in . |
| Sol.
|
| Q16. If , , and are square matrices of the same order, then always implies that . |
| Sol.
|
| Q17. is always a symmetric matrix for any matrix . |
| Sol.
|
Q18. If 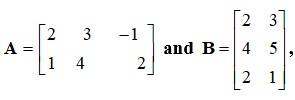 then
and
are defined and equal. then
and
are defined and equal. |
| Sol. |
| Q19. If is a skew symmetric matrix, then is a symmetric matrix. |
| Sol.
|
| Q20. , where and are invertible matrices satisfying the commutative property with respect to multiplication. |
| Sol.
|
Commonly asked questions
A matrix denotes a number.
This is a True or False Type Questions as classified in NCERT Exemplar
Matrices of any order can be added.
This is a True or False Type Questions as classified in NCERT Exemplar
Matrices of different orders cannot be subtracted
This is a True or False Type Questions as classified in NCERT Exemplar
Matrix addition is associative as well as commutative.
This is a True or False Type Questions as classified in NCERT Exemplar
Matrix multiplication is commutative.
This is a True or False Type Questions as classified in NCERT Exemplar
A square matrix where every element is unity is called an identity matrix.
This is a True or False Type Questions as classified in NCERT Exemplar
Two matrices are equal if they have the same number of rows and the same number of columns.
This is a True or False Type Questions as classified in NCERT Exemplar
If and are two square matrices of the same order, then .
This is a True or False Type Questions as classified in NCERT Exemplar
If and are two matrices of the same order, then
This is a True or False Type Questions as classified in NCERT Exemplar
If matrix , then or or both and are null matrices.
This is a True or False Type Questions as classified in NCERT Exemplar
Transpose of a column matrix is a column matrix.
This is a True or False Type Questions as classified in NCERT Exemplar
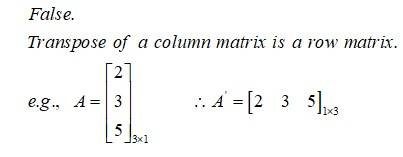
If and are two square matrices of the same order, then .
This is a True or False Type Questions as classified in NCERT Exemplar
If each of the three matrices of the same order is symmetric, then their sum is a symmetric matrix.
This is a True or False Type Questions as classified in NCERT Exemplar
If and are any two matrices of the same order, then .
This is a True or False Type Questions as classified in NCERT Exemplar
If , where and are not square matrices, then the number of rows in is equal to the number of columns in and the number of columns in is equal to the number of rows in .
This is a True or False Type Questions as classified in NCERT Exemplar
If , , and are square matrices of the same order, then always implies that .
This is a True or False Type Questions as classified in NCERT Exemplar
is always a symmetric matrix for any matrix .
This is a True or False Type Questions as classified in NCERT Exemplar
If 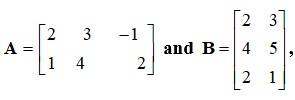 then and are defined and equal.
then and are defined and equal.
This is a True or False Type Questions as classified in NCERT Exemplar

If is a skew symmetric matrix, then is a symmetric matrix.
This is a True or False Type Questions as classified in NCERT Exemplar
, where and are invertible matrices satisfying the commutative property with respect to multiplication.
This is a True or False Type Questions as classified in NCERT Exemplar
24th June 2022 (second shift)
24th June 2022 (second shift)
Commonly asked questions
Let x * y = x2 + y3 and (x * 1) * 1 = x * (1 * 1). Then a value of 2 is.
The sum of all the real roots of the equation
=
Let the system of linear equations
x + y +
3x + y + z = 4
x + 2z = 1
have a unique solution If are collinear points, then the sum of absolute values of all possible values of is
x + y + az = 2………… (i)
3x + y + z = 4 ………… (ii)
x + 2z = 1 ……………. (iii)
x = 1, y = 1, z = 0
(for unique solution
are collinear.
Sum of absolute value = 2
Let x,y > 0. If x3y2 = 215, then the least value of 3x + 2y is
Let f(x)
where [t] denotes greatest integer If m is the number of points where f is not continuous and n is the number of points where f is not differentiable, then the ordered pair (m, n) is
Hence f (x) is not differentiable at x = 1, 0, 1
The value of the integral
……. (i)
S =
A particle is moving in the xy-plane along a curve C passing through the point (3, 3). The tangent to the curve C at the point P meets the x-axis at Q. If the y-axis bisects the segment PQ, then C is a parabola with
Equation of tangent at P (x, y) is Y =
It passes through (3, 3), c = 3
Length of latus rectum = 3
Let the maximum area of the triangle that can be inscribed in the ellipse having one of its vertices at one end of the major axis of the ellipse and one of its sides parallel to the y-axis, be . Then the eccentricity of the ellipse is
Let the area of the triangle with vertices A be 4 sq. units. If the points are collinear, then is equal to
are collinear.
The number of distinct real roots of the equation x7 – 7x – 2 = 0 is
Hence number of real roots of f (x) = 0 are 3.
A random variable X has the following probability distribution
x is a random variable.
The number of solutions of the equation
total number of solution = 7.
If the shortest distance between the lines and then the sum of all possible values of is
S. D. =
Let the points on the plane P be equidistance from the points (–4, 2, 1) and (2, –2, 3). Then the acute angle between the plane P and the plane 2x + y + 3z = 1 is
Let P (x, y, z) be any point on plane P1 then
Let and be two unit vectors such that = 2. If is the angle between , then among the statements:
(S1) : The projection of
squaring on both sides, we get =
where θ is angle between
is correct.
and projection of
So (S2) is correct.
If y = tan-1 (sec x3 tanx3),
Consider the following statements:
A : Rishi is a judge.
B : Rishi is honest.
C : Rishi is not arrogant.
The negation of the statement “if Rishi is a judge and he is not arrogant, then he is honest” is
given statement is
then its negation is
The slope of normal at any point (x,y), X > 0, y > 0 on the curve y = y(x) is given by If the curve passes through the point (1, 1), then e.y (e) is equal to
Put x = 1, y = 1
Let be the largest value of for which the function is increasing for all Then is equal to
For increasing
Let S = If is the point in S which in closest to 4i, then 25 is equal to
Circle
and line
Let and let Tn = Then the number of elements in
then even power of A as A =
If b = 1 & and n (n + 1) is always even
are all 1 for b = 1 and each value of a.
The number of 7-digit numbers which are multiples of 1 and are formed using all the digits 1, 2, 3, 4, 5, 7 and 9 is
Sum of all given numbers = 31
Difference between odd and even positions must be 0,11 or 22 but 0 and 22 are not possible.
Hence 11 is possible.
This is possible only when either 1, 2, 3, 4 if filled in odd places in order and remaining in other order.
Hence 2, 3, 5 or 7, 2, 1 or 4, 5, 1 at even places.
Total possible ways = (4! × 3!) × 4 = 576
The sum of all elements of the set is
HCF of (a, 24) = 1 a = 1, 5, 7, 11, 13, 17, 19, 23 sum of these numbers = 96
There are four such blocks and a number 97 is there upto 100.
complete sum = 96 + (24 × 8 + 96) + (48 × 8 + 96) + (72 × 8 + 96) + 97 = 1633
The remainder on diving 1 + 3 + 32 + 33 + …. + 32021 by 50 is
S = 1 + 3 + 32 + 33 + ….+ 32021
= 50k1 + 4
Remainder = 4
The area (in sq. units) of region enclosed between the parabola y2 = 2x and the line x + y = 4 is
Required area
=
=
Let a circle C : touch the axis (1,0). If the line x + y = 0 intersects the circle C at P and Q such that the length of the chord PQ is 2, then the value of h + k + r is equal to
OM2 = OP2 = PM2
equation of circle is
In an examination, there are 1- true-false type questions. Out of 10, at student can guess the answer of 4 questions correctly with probability and the remaining 6 questions correctly with probability . If the probability that the student guesses the answer of exactly 8 questions correctly out of 10 is then k is equal to
Since student guesses only two wrong. So there are three possibilities
(i) both wrong in section A
(ii) both wrong in section B
(iii) one wrong in each section A and B.
Required possibilities =
Let the hyperbola and the ellipse E : 3x2 + 4y2 = 12 be such that the length of latus rectum of H is equal to the length of latus rectum of E. If eH and eE are the eccentricities of H and E respectively, then the value of is equal to
Length of latus rectum =
length of latus rectum = = 3
= 12 ×
Let P1 be a parabola with vertex (3, 2) and focus (4, 4) and P2 be its mirror image with respect to the line x + 2y = 6. Then the directrix P2 is x + 2y =.............
S (4, 4) and V (3, 2)
point of intersection of directrix with axis of parabola is A (2, 0)
Image of A (2, 0) with respect to line
Point B is point of intersection of directrix with axes of parabola P2.
lies on the line x + 2y =
JEE Mains Solutions 2022,28th june , Maths,Second shift
JEE Mains Solutions 2022,28th june , Maths,Second shift
Commonly asked questions
Let R1 =
R2 = Then on N :
R1 =
But it is not necessary that if (a,b) & (b, c)
Eg
R2 =
But it is not necessary that if (a, b) & (b, c) then (a, c) also .
Eg – (21, 1)
let f(x) be a quadratic polynomial such that f(-2) + f(3) = 0. If one of the roots of f(x) = 0 is -1, then the sum of the roots of f(x) = 0 is equal to:
Let’s assume other root to be a
Given that f (-2) + f (3) = 0
a (-2 + 1) (-2 -a) + a (3 + 1) (3 - a) = 0
Þ 14 -3a = 0 Þ a =
sum of roots =
The number of ways to distribute 30 identical candies among four children C1, C2, C3 and C4 so that C2 receives atleast 4 and atmost 7 candies, C3 receives atleast 2 and atmost 6 candies, is equal to:
Let the number of chocolates given to C1, C2, C3 & C4 be a, b, c, d respectively.
Given 4
Now using these the maximum number of chocolates that can be given to C1 or C4 is 24 (where b & c are given 2 & 4 chocolates).
& a + b + c + d = 30
So, total possible solution to the above equation.
Coefficient of x30 in.
=
x56 & x31 can never give x30 so we discard them.
Coefficient x30 ® 18C3 – 23C3 – 22C3 + 27C3
=
= 430
The term independent of x in the expansion of
(r + 1)th term for expansion of
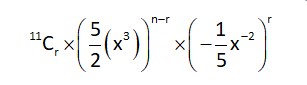
r = y
= 11Cy
for term to be independent of x, power of x should be zero.
(3x – 2y) = 0 (when 1 is multiplied).
3x + 3y = 33
y =
3x – 2y + 2 = 0 where (-x2) is multiplied).
3x + 3y = 33
y = 7, x = 4
coefficient of term independent of x.
If n arithmetic means are inserted between a and 100 such that the ratio of the first mean to the first mean to the last mean is 1 : 7 and a + n = 33, then the value of n is:
a + a1……an, 100 n arithmetic mean 100
a + n = 33 ……. (i)
7a + 8d = 100…………… (ii)
a + (n + 1)d = 100………………. (iiI)
Solving these equations (i), (ii) & (iii), we get
n = 23 & d =
a = 10
Let f, g : R ® R be functions defined by
where [x] denote the greatest integer less than or equal to x. Then, the function fog is discontinuous at exactly:
fog
Not possible as of inequalities give
ex – x < 0, x < 0 (x – 1)2 – 1 < 0
Not possible (x – 1 + 1)(x – 1 – 1) < 0
(x)(x – 2) < 0
x
continuous x < 0
Discontinuous at 0
continuous
fog is discontinuous at 0
Let f : R ® R be a differentiable function such that and let Then is equal to:
g(x)
=
=
Let f : R® R be a continuous function satisfying f(x) + f(x + k) = n, for all x R where k > 0 and n is a positive integer. If
Replace x by x + k.
From (i) & (ii), f(x + 2k) = f(x).
is periodic with period = 2k.
put x = t + k
The area of the bounded region enclosed by the curve y = 3 - and the x-axis is:
Graph
Area =
Let x = x(y) be the solution of the differential equation 2y such that x(1) = 0. Then, x(e) is equal to:
Integrating
y = 1, n = 0 c = 2
x = -e2 In2
Let the lope of the tangent to a curve y = f(x) at (x,y) be given by 2 tan x (cos x – y). If the curve passes through the point then the value of is equal to:
Solution y sec2x =
y sec2 x = 2sec x + c
y = 2 cos x + c cos2x passes C =
y = 2 cos x
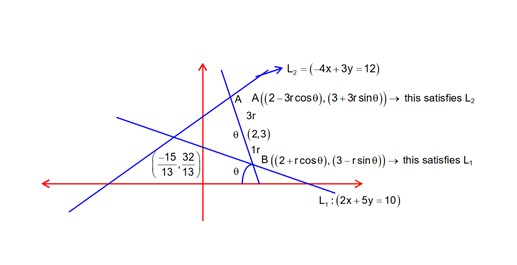
Let a triangle be bounded by the lines L1 : 2x + 5y = 10; L2 : -4x + 3y = 12 and the line L3, which passes through the point P(2, 3), intersects L2 at A and L1 at B. If the point P divides the line-segment AB, internally in the nation 1 :3, then the area of the triangle is equal to:
Let a > 0, b > 0. Let a and respectively be the eccentricity and length of the latus rectum of the hyperbola Let e’ and respectively be the eccentricity and length of the latus rectum of its conjugate hyperbola. If then the value of 77a + 44b is equal to
65b2 = 44b3
65 = b × 44
Let If the area of the parallelogram whose adjacent sides are represented by the vectors then the value of is equal to:
=
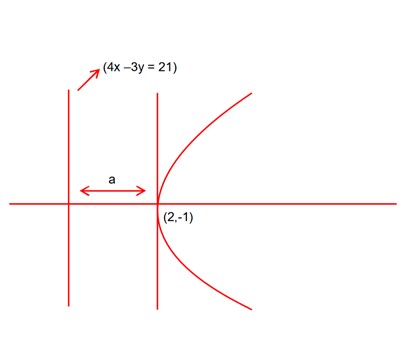
If vertex of a parabola is (2, -1) and the equation of its directrix is 4x – 3y = 21, then the length of its latus rectum is:
Let the plane ax + by + cz = d pass through (2, 3, -5) and its perpendicular to the planes
2x + y – 5z = 10 and 3x + 5y – 7z = 12.
If a, b, c, d are integers d > 0 and then the value of a + 7b + c + 20d is equal to:
ax + by + cz = d
2a + 3b – 5c = d 2a + 3b – 5c = d …………….(v)
Putting (i) & (iv) in (v) we get a = -9d.
In conditions
2b = d …………...(i) d > 0
2a + b – 5c = 0 2a + 3b – 5c = d
=
3a + 5b – 7c = 0) ×
c = -7, d = 2
(iii)…(ii) ® 2a + 3b
2a + 3b =
Putting values
a + 7b + c + 20d = 22
The probability that a randomly chosen one-one function from the set to the set satisfies f(a) + 2f(b) – f(c) = f(d) is:
No of one – one functions ® 5P4 = 120
f(a) + 2f(b) – f(c) = f(d)
2f(b) = f(d) + f(c) – f(a)
So, f(d) + f(c) – f(a) should be even.
Only possibilities of f(d) f(c) f(a)
Not possible since E E E E - even, O – Odd
function is one one E O O
O O E
O E O
Case (i)
f(d) f(c) f(a)
E O O
2 1 3 similarly we write cases for f(d) = 4
2 1 5 413
2 3 5 431
2 5 1 435
2 3 1 453
2 5 3 415
4512222asdf=fhf=kjhfjkdfh45654hdfkjdhjh
Case (ii)
O O E O O E
1 5 2 1 5 4
5 1 2 5 1 4
3 1 2 1 3 4
1 3 2 3 1 4
3 5 2 5 3 4
5 3 2 &nb
The value of is equal to:
Let be a vector which is perpendicular to the vector If then the projection of the vector on the vector is:
Let
4x – 12 = 0 y = 2
x = 3
z = -5
x -2z = 13
If cot a = 1 and sec b = , where then the value of tan(a + b) and the quadrant in which a + b lies, respectively are:
cota = 1 & secβ =
< < secβ =
cosβ =
tanb =
tan(α + β) =
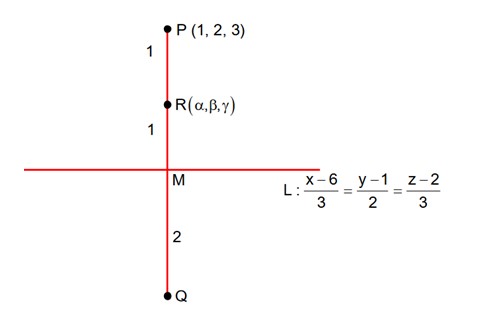
Let the image of the point P(1, 2, 3) in the line be Q . be a point that divides internally the line segment PQ in the ration 1 : 3. Then the value of is equal to………….
Any point on line L is
M (3r + 6, 2r + 1, 3r + 2)
Suppose a class has 7 students. The average marks of these students in the mathematics examination is 62, and their variance is 20. A student fails in the examination if he/she gets less than 50 marks, then in worst case, the number of students can fail is…………..
= 140……………… (i)
If any one student get less 50 marks then
but
both condition cannot satisfy together hence no students fails.
If one of the diameters of the circle is a chord of circle. then the value of r2 is equal to…………….
centre
radius
centre
OA =
r2 =
If then the value of (a – b) is equal to………….
For this limit to be defined 2x3 – 7x2 + ax + b should also trend to 0 or x ® 1.
2 – 7 + (a + b) = 0
(a + b) = 5 …………….(i)
Now this becomes % form we apply L’lopital rule
Now the numerator again ® 0 as x = 1
6x2 – 14x + a ® 0 as x = 1
6 . (1)2 – 14 + a = 0
a = 8 …………….(ii)
a + b = 5
(b = -3) ® from (i) & (ii)
Let for n = 1, 2,……, 50, Sn be the sum of the infinite geometric progression whose first term is n2 and whose common ratio is Then the value of is equal to…………..
If the system of linear equations
2x – 3y = = 5,
aX + 5y = b + 1, where has infinitely many solutions, then the value of is equal to…………..
(i)
5x + 25 = -3β - 3
=
Let A = where i Then, the number of elements in the set is…………….
A9 = A
total possible values of n = 25
Sum of squares of modulus of all the complex numbers z satisfying is equal to…………..
Let z be equal to (x + iy)
(x + iy) + (x – iy) = (x + iy)2 (i + 1)
Equating the real & in eg part.
(i) & (ii)
4xy = -2x Þ x = 0 or y =
(for x = 0, y = 0)
For y =
x2
x =
=
of
=
Let S = Then the number of elements in the set is……………….
(2, 1) (1, 2), (2, 2) each element has 3 choice.
(3, 2) (2, 3) (3, 1) (1, 3) (3, 3) each element has two choices.
total function = 3 × 3 × 2 × 2 × 2 = 72
Case I
None of the pre image have 3 as image, total functions = 2 × 2 × 1 × 1 × 1 = 4
Case II
None of the pre images have 2 as image then number of function = 25 = 32
Case III
None of the pre image have either 3 or 2 as image
Total function = 15 = 1
Total number of onto function
= 72 – 4 – 32 + 1 = 37
The maximum number of compound propositions, out of that can be made simultaneously true by an assignment of the truth values to p, q, r and s, is equal to………….
p q r s
F T F
Maths NCERT Exemplar Solutions Class 12th Chapter Three Exam