Maths
Get insights from 6.5k questions on Maths, answered by students, alumni, and experts. You may also ask and answer any question you like about Maths
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
3 months agoContributor-Level 10
Let the equation of normal is Y – y = -
where m is slope of tangent to the given curve then
It passes through (a, b) so b – y =
->(a – x) dx = (y – b) dy
On integration
(ii) passes through (3, -3) & then
3a – 3b – c = 9 .(ii)
& 4a - - c = 12 .(iii)
also given
Solve (ii), (iii) & (iv) b = 0, a = 3
Hence a2 + b2 + ab = 9
New answer posted
3 months agoContributor-Level 10
Given
put 1 - x =
dx = -dt
From (i)
(i)
Similarly by (ii)
Adding (iii) & (iv)
Putting
Hence dx = a lm, n
-> a = 1
New answer posted
3 months agoContributor-Level 10
Kindly go throuigh the solution
Given
&
(i) & (ii)
Now variance = 1 given
->(a - b) (a - b + 4) = 0
Since
New answer posted
3 months agoContributor-Level 10
Given
So at least one root will lie in (-2, -1)
now
So, f(x) be purely increasing function so exactly one root of f(x) that will lie in (-2, 1). Hence |a| = 2
New answer posted
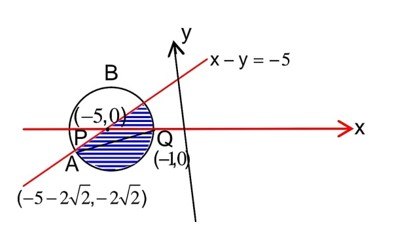
3 months agoLet z be those complex numbers which satisfy
If the maximum value of then the value of (a + b) is…….
Contributor-Level 10
->Represent a circle
->Represent a line X – y
So max |z + 1|2 = AQ2
Hence a + b = 48
New answer posted
3 months agoContributor-Level 10
Given
Now quadratic equation having roots a & b will be x2 – (a + b)x + ab = 0
i.e. x2 – x – 1 = 0, put x = a and put x = b
So a2 = a + 1 & b2 = b + 1
(i)
->
New answer posted
3 months agoContributor-Level 10
18 = 32 * 2
For G.C.D to be 3. no. of four digits should be only multiple of 3, but not multiple of 9 & also should not be even.
As we know no. of the form
9 k -> 1000
9 k + 1 -> 1000
9 k + 2 -> 1000
9 k + 3 -> 1000 -> Total no. = 2000
9 k + 4 -> 1000
9 k + 5 -> 1000
9 k + 6 ->1000
9 k + 7 -> 1000
9 k + 8 -> 1000
In which half will be even & half be odd so Required no. = 1000
New answer posted
3 months agoContributor-Level 10
Given sequence is -16, 8, -4, 2, .
are in G.P. with first term a = -16 & common ratio r =
Now
So A.M. = -8
Given equation is 4x2 – 9x + 5 = 0 gives
From roots we get possible value of b = 1 so
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
