Maths
Get insights from 6.5k questions on Maths, answered by students, alumni, and experts. You may also ask and answer any question you like about Maths
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
6 months agoContributor-Level 10
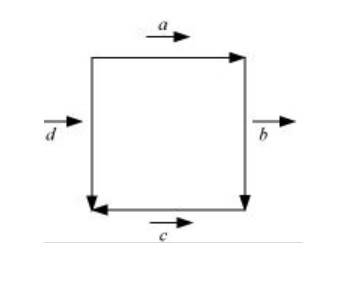
(i) True, as vector quantity and - are parallel to same line.
(ii) False, as collinear vector are those vectors that are parallel to same line, but it is not necessary that they are equal also.
(iii) False, as two vectors having same magnitude may have different directions, so they are not collinear.
(iv) False, as two collinear vectors having same magnitude are not equal whey they are opposite in direction.
New answer posted
6 months agoContributor-Level 10
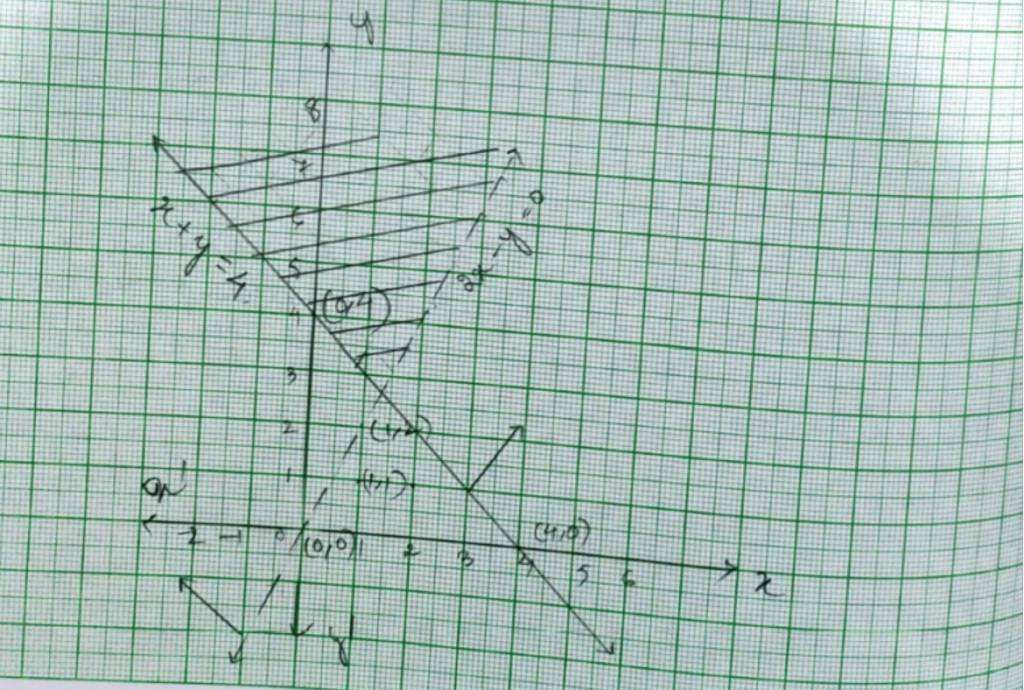
41. The given system of inequality is
2x – y> 1 - (1)
x – 2y< 1- (1)
So the corresponding equations are
2x – y=1
x | 0 | 0.5 |
y | –1 | 0 |
and x – 2y= –1
x | –1 | 0 |
y | 0 | 0.5 |
Putting (x, y)= (0,0) in (1) and (2) to cheek the inequality
2 * 0 – 0 > 1
0 > 1 which is not true.
and 0 – 2 * 0< 1
0< 1 which is not true.
So, the solution of plane of inequality (1)and (2) does not include the plane with point (0,0) or origin.
? The reqd. solution of the given system of inequality is the shaded region.

New answer posted
6 months agoContributor-Level 10

(a) Vector and are co initial same initial point.
(b) and same magnitude & direction.
(c) and are collinear but not equal they are parallels their direction are not same.
New answer posted
6 months agoContributor-Level 10
(i) Time period involves only magnitude. So, it is scalar quantity.
(ii) Distance involves only magnitude. So, it is scalar quantity.
(iii) Force involves both magnitude and direction. So, it is vector quantity.
(iv) Velocity involves both magnitude and direction. So, it is vector quantity.
(v) Work done involves only magnitude. So, it is scalar quantity.
New answer posted
6 months agoContributor-Level 10
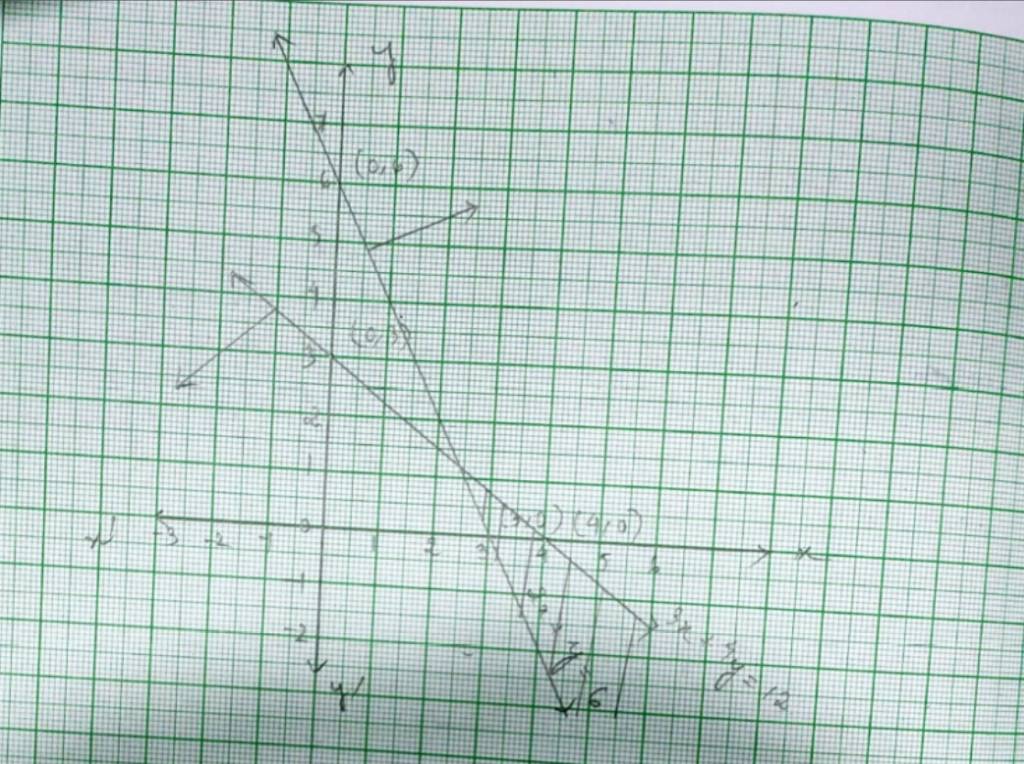
40. The given system of inequalities is
x + y ≥ 4.- (1)
2x – y< 0.- (2)
The corresponding equations are x+y=4 and 2x – y=0.
x | 0 | 4 |
y | 4 | 0 |
and
X | 0 | 1 |
Y | 0 | 2 |
Put (x, y)= (1,1) in (1) and (2).
So, 1+1 ≥ 4
2 ≥ 4 which is not true.
and 2 * 1 – 1<0
1<0 which is not true.
So solution of plane of inequality (1) and (2) does not include the plane with point (1,1).
? The reqd. solution of the given system of inequality is the shaded portion.
New answer posted
6 months agoContributor-Level 10
(i) 10kg involves only magnitude. So, it is scalar quantity.
(ii) 2 meters north-west involves both magnitude and direction. So, it is vector quantity.
(iii) 400 involves only magnitude. So, it is scalar quantity.
(iv) 400 watts involves only magnitude. So, it is scalar quantity.
(v) 10-19 coulomb involves only magnitude. So, it is scalar quantity.
(vi) 20m/s-2 involves magnitude and direction. So, it is vector quantity.
New answer posted
6 months agoContributor-Level 10
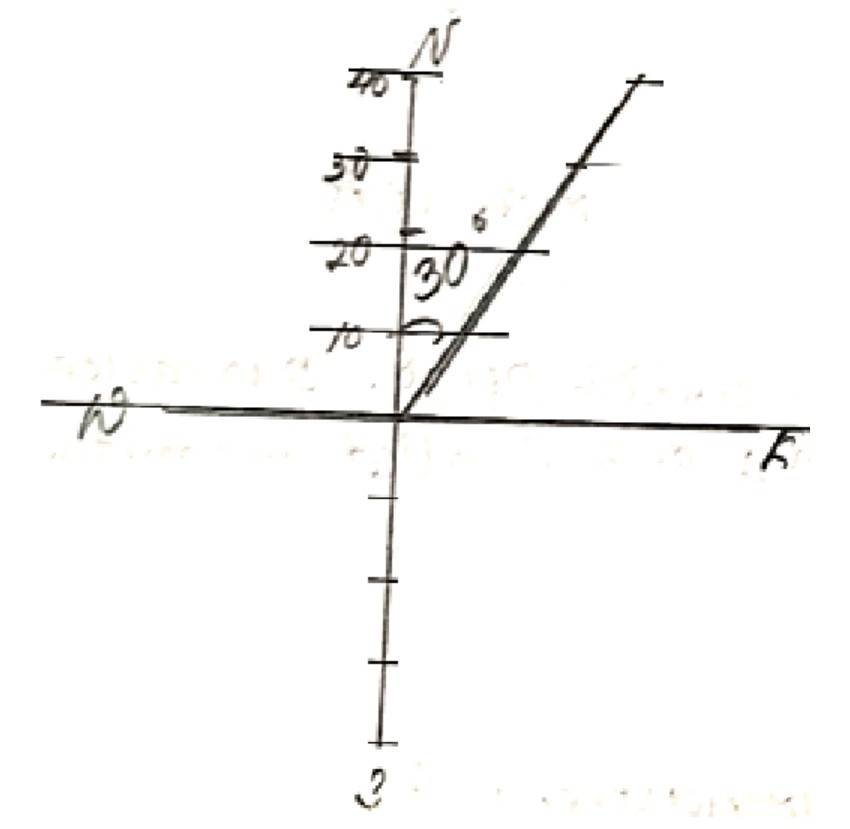
39.The given system of inequalities is
2x+y ≥ 6 - (1)
3x+4y ≤ 12- (2)
The corresponding equations are
2x + y = 6
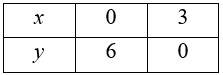
and 3x + 4y = 6
So,
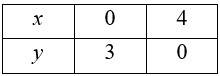
Put (x, y)= (0,0) in (1), (2),
? 2 * 0+0 ≥ 6
0 ≥ 6 which is false.
And 3 * 0+4 * 0 ≤ 12
0 ≤ 12 which is true.
So, solution of inequality (1) lies on the plane which excludes the origin and the solution of inequality (2) lies on
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 679k Reviews
- 1800k Answers