Maths

13. $\underset{x\to 0}{lim}\frac{sinax}{bx}=\frac{1}{b}\underset{x\to 0}{lim}\frac{sinax}{ax}*a$

$=\frac{a}{b}\underset{x\to 0}{lim}\frac{sinax}{ax}$ 

$=\frac{a}{b}$

Kindly go through the solution

$=\frac{1}{2*(-2)}=-\frac{1}{4}.$

11. $\underset{x\to 1}{lim}\frac{a{x}^2+bx+c}{c{x}^2+bx+a}=\frac{a+b+c}{c+b+a}=1$

10.$=\underset{z\to 1}{lim}\left[\frac{z^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}-1^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{z-1}\right]÷\underset{z\to 1}{lim}\left[\frac{z^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}-1^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}}{z-1}\right]$

$=\underset{z\to 1}{lim}\left[\frac{z^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}-1^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{z-1}\right]÷\underset{z\to 1}{lim}\left[\frac{z^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}-1^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}}{z-1}\right]$

We know that,

$\underset{}{}$$\underset{x\to a}{lim}\frac{x^n-a^n}{x-a}=n{a}^{n-1}$

So,

$=\frac{1}{3}*6=2$

Kindly go through the solution

8.

$=\underset{x\to 3}{lim}\frac{(x+3)(x^2+9)}{2x+1.}$

$=\frac{(3+3)\left(3^2+9\right)}{2*3+1}$

$=\frac{6*18}{6+1}$

$=\frac{108}{7}$

33. In the word EQUATION, there are vowels (E, U, A, I, O) and 3 consonants (Q, T, N).

Treating vowels as a whole as 1st object and consonants as a whole as 2nd object, we can have an arrangement of 2! = 2.

Similarly, arrangement within the vowels = 5! = 5 * 4 * 3 * 2 * 1 = 120

And arrangement within the consonants = 3! = 3 * 2 * 1 = 6

Therefore, total number of possible arrangement = 2 * 120 * 6 = 1440

7.

32. In the word DAUGHTER, there are 3 vowels, namely A, U, E and 5 consonants, namely D, G, H, T, R.

The number of ways of selecting 2 vowels out of 3

= ³C₂

= $\frac{3!}{2!\left(3-2\right)!}$

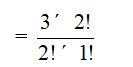
= 3

The number of ways of selecting 3 consonants out of 5

= ⁵C₃

= $\frac{5!}{3!\left(5-3\right)!}$

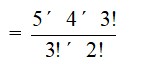
= 5 * 2

= 10

Therefore, the number of combination of 3 consonants and 2 vowels is 3 * 10 = 30.

Each of these 30 combinations has 5 letters which can be arranged among themselves in 5! Ways.

Therefore, the required numbers of different words is

= 30 * 5! = 30 * 5 * 4 * 3 * 2 * 1 = 3600

31. A student can choose 5 out of 9 available courses. However 2 specific courses are made compulsory.

So, now a student has 3 choices out of the remaining 7 courses.

Therefore, the required number of ways

=⁷C₃

= $\frac{7!}{3!\left(7?3\right)!}$

= 35