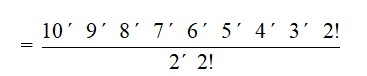Maths

23. Given f (x) $\{\begin{array}{ll}2x+3,\hfill & x\le 0\hfill \\ 3(x+1),\hfill & x>0\hfill \end{array}\}$

for $\underset{x\to 0}{lim}f(x),$

left hand limit, L.H.S = $\underset{x\to 0^{}}{lim}f(x)$ = $\underset{x\to 0^{}}{lim}(2x+3)$

= 2 0 + 3 = 3.

Right hand limit, R.H.L = $\underset{x\to 0^{+}}{lim}f(x)=\underset{x\to 0^{+}}{lim}3(x+1)$

= (0 + 1) = 3 1 = 3.

Thus, $\underset{x\to 0^{-}}{lim}f(x)=\underset{x\to 0^{+}}{lim}f(x)=\underset{x\to 0^{-}}{lim}f(x)=3$

For $\underset{x\to 1}{lim}f(x),$

L.H.L = $\underset{x\to 1^{-}}{lim}f(x)=\underset{x\to 1^{-}}{lim}3(x+1)=3(1+1)=3*2=6$

R.H.L = $\underset{x\to 1^{+}}{lim}f(x)=\underset{x\to 1^{+}}{lim}3(x+1)=3(1+1)=3*2=6.$

Thus, $\underset{x\to 1^{-}}{lim}f(x)=\underset{x\to 1^{+}}{lim}f(x)=\underset{x\to 1}{lim}f(x)=6.$

22. $\underset{x\to \raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{lim}\frac{tan2x}{x-\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$

Put y = x $\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ . So that as y 0 cos $\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.$

21. $\underset{x\to 0}{lim}(cosecx-cotx)=\underset{x\to 0}{lim}\left(\frac{1}{sinx}-\frac{cosx}{sinx}\right)$

$=\underset{x\to 0}{lim}\left(\frac{1-cosx}{sinx}\right)$

$=\underset{x\to 0}{lim}\frac{2si{n^2}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{2si{n}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}co{s}^{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$ $\{\begin{array}{}\end{array}?cos2x=1-2si{n}^{2}x\Rightarrow 1-cos2x=2si{n}^{2}x1-cosx=2si{n}^2\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2$}\right.?sin2x=2sinxcosxsinx=2sin\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2$}\right.cos\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\{$

$=\underset{x\to 0}{lim}\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$

$=tan\raisebox{1ex}{$0$}\!\left/ \!\raisebox{-1ex}{$2$}\right.=0.$

20. $\underset{x\to 0}{lim}\frac{sinax+bx}{ax+sinbx}=\frac{\underset{x\to 0}{lim}\frac{sinax}{ax}*ax+bx}{\underset{x\to 0}{lim}ax+\frac{sinbx}{bx}*bx}.$

$\frac{\underset{x\to 0}{lim}\frac{sinax}{ax}*\underset{x\to 0}{lim}ax+\underset{x\to 0}{lim}bx}{\underset{x\to 0}{lim}ax+\underset{x\to 0}{lim}\frac{sinbx}{bx}*\underset{x\to 0}{lim}bx}$

$=\frac{\underset{x\to 0}{lim}ax+\underset{x\to 0}{lim}bx}{\underset{x\to 0}{lim}ax+\underset{x\to 0}{lim}bx}$

$=\underset{x\to 0}{lim}\frac{ax+bx}{ax+bx}$

$=\underset{x\to 0}{lim}1$

= 1.

19. $\underset{x\to 0}{lim}xsecx=\underset{x\to 0}{lim}\frac{x}{cosx}$

$=\frac{0}{cos0}$

$=\frac{0}{1}$

= 0.

35. Since the 6-digit numbers to be formed from the digits 0, 1, 3, 5, 7 and 9 has to be divisible by 10 we have to fix the unit place as 0. Now, the remaining 5 places can be filled only by the digits 1, 3, 5, 7 and 9.

Therefore, the required number of ways

= 5!

= 5 * 4 * 3 * 2 * 1

= 120

16. $\underset{x\to 0}{lim}\frac{cosx}{\pi -x}=\frac{cos0}{\pi -0}=\frac{1}{\pi }$

15. $\underset{x\to \pi }{lim}\frac{sin(\pi -x)}{\pi (\pi -x)}=\frac{1}{\pi }*\underset{x\to \pi }{lim}\frac{sin(\pi -x)}{\pi -x}$

$=\frac{1}{\pi }.$

14. $\underset{x\to 0}{lim}\frac{sinax}{sinbx}=\underset{x\to 0}{lim}\frac{\frac{sinax}{ax}*ax}{\frac{sinbx}{bx}*bx}$

$=\frac{a}{b}$

34. In the eleven-letter word EXAMINATION there are 2A's, 2I's and 2N's and the rest are all different.

Since in a dictionary the words are listed according to the English alphabet we can only find words starting with A (as B, C, D are not a part of the letters forming the word EXAMINATION) listed before E.

Hence after fixing one A as first word we can rearrange the remaining 10 letters of which 2 are I, 2 are N and rest are all different.

Therefore, the required number of ways = $\frac{10!}{2! 2!}$

= 10 * 9 * 8 * 7 * 6 * 5 * 2 * 3

= 9,07,200