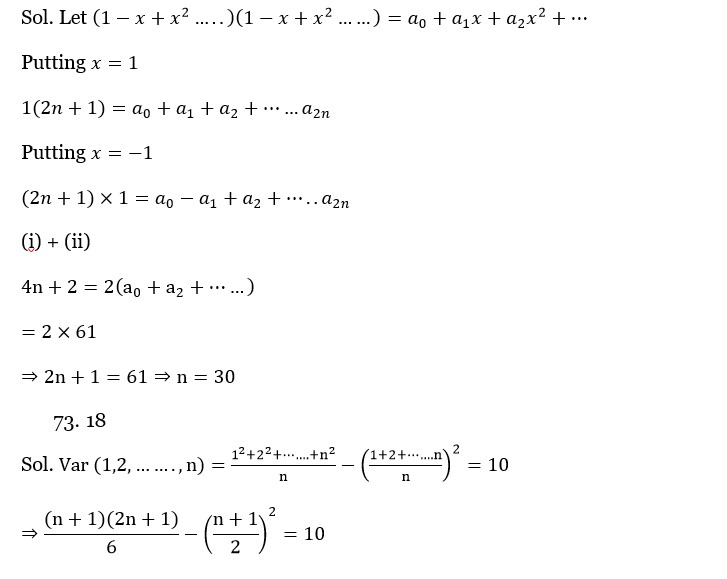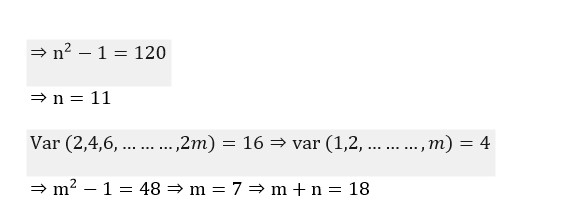Maths
Get insights from 6.5k questions on Maths, answered by students, alumni, and experts. You may also ask and answer any question you like about Maths
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
2 months agoContributor-Level 9
A = lim (n→∞) (2/n) ∑ (r=1 to n) f (r/n + n/ (n²)
(The term n/n² seems intended to be part of the function argument, not simply added. The solution proceeds as if it's f (r/n)
A = lim (n→∞) (2/n) ∑ (r=1 to n) [ f (r/n) + f (1/n) + . + f (n-1)/n) ]
The expression in the image seems to be: A = lim (n→∞) (2/n) [ f (1/n) + f (2/n) + . + f (n-1)/n) ]
A = 2 ∫? ¹ f (x) dx = 2 ∫? ¹ log? (1 + tan (πx/4) dx
put πx/4 = t ⇒ dx = 4/π dt
A = 2 ∫? ^ (π/4) log? (1 + tan (t) * (4/π) dt = (8/π) ∫? ^ (π/4) log? (1 + tan (t) dt
Using the property ∫? f (x)dx = ∫? f (a-x)dx, the integral ∫? ^ (π/4) log (1 + tan (t)dt ev
New answer posted
2 months agoContributor-Level 9
lim (x→0) [a e? - b cos (x) + c e? ] / (x sin (x) = 2
Using Taylor expansions around x=0:
lim (x→0) [a (1+x+x²/2!+.) - b (1-x²/2!+.) + c (1-x+x²/2!+.)] / (x * x) = 2
lim (x→0) [ (a-b+c) + x (a-c) + x² (a/2+b/2+c/2) + O (x³)] / x² = 2
For the limit to exist, the coefficients of lower powers of x in the numerator must be zero.
a - b + c = 0
a - c = 0 ⇒ a = c
Substituting a=c into the first equation: 2a - b = 0 ⇒ b = 2a.
The limit becomes: lim (x→0) [x² (a/2 + b/2 + c/2)] / x² = (a+b+c)/2
(a + b + c) / 2 = 2 ⇒ a + b + c = 4.
New answer posted
2 months agoContributor-Level 9
|z+i|/|z-3i| = 1 ⇒ |z+i| = |z-3i|. This means z is on the perpendicular bisector of the segment from -i to 3i. The midpoint is i, so z = x+i.
w = z? - 2z + 2. Let z = x + iy.
w = (x² + y²) - 2 (x + iy) + 2 = (x² - 2x + 2 + y²) - 2iy.
Re (w) = x² - 2x + 2 + y² = (x - 1)² + 1 + y².
From the first condition, y=1. Re (w) = (x - 1)² + 1 + 1 = (x - 1)² + 2.
Re (w) is minimum for x = 1.
The common z is z = 1 + i.
w = (1+i) (1-i) - 2 (1+i) + 2 = 2 - 2 - 2i + 2 = 2 - 2i.
w² = (2 - 2i)² = 4 (1 - 2i - 1) = -8i.
w? = (-8i)² = -64 ∈ R.
∴ least n ∈ N for which w? ∈ R is n=4.
New answer posted
2 months agoContributor-Level 10
P will be the centroid of triangle ABC.
The centroid P is (x? +x? +x? )/3, (y? +y? +y? )/3).
The coordinates of P are given as (17/6, 8/3).
The coordinates of Q are not given, but a calculation is shown.
PQ = √ (24/6)² + (9/3)²) = √ (4² + 3²) = √ (16+9) = √25 = 5.
This implies the coordinates of Q are such that the difference in coordinates with P leads to this result. For example if P= (x? , y? ) and Q= (x? , y? ), then x? -x? =4 and y? -y? =3.
New answer posted
2 months agoContributor-Level 9
dy/dx = 2 (x + 1)
dy = 2 (x + 1)dx.
y = (x + 1)² - c (1)
For y = 0, (x+1)² = c ⇒ x = -1 ± √c.
Area A = ∫? √c? ¹? √c (0 - [ (x+1)² - c])dx = ∫? √c? ¹? √c (c - (x+1)²)dx
A = [cx - (x+1)³/3] from -1-√c to -1+√c
= (c (-1+√c) - (√c)³/3) - (c (-1-√c) - (-√c)³/3)
= -c+c√c - c√c/3 + c+c√c - c√c/3 = 2c√c - 2c√c/3 = (4/3)c√c.
Given A = 4√8 / 3 = 8√2 / 3.
(4/3)c^ (3/2) = 8√2 / 3 ⇒ c^ (3/2) = 2√2 = 2^ (3/2) ⇒ c = 2.
∴ y = (x + 1)² - 2.
∴ y (1) = (1 + 1)² - 2 = 2.
New answer posted
2 months agoContributor-Level 10
Let t = 3^ (x/2). As x→2, t→3^ (2/2) = 3.
The limit becomes lim (t→3) [ (t² + 27/t²) - 12 ] / [ (t - 3²/t) ].
lim (t→3) [ (t? - 12t² + 27)/t² ] / [ (t² - 9)/t ].
lim (t→3) [ (t²-9) (t²-3) / t² ] * [ t / (t²-9) ].
lim (t→3) [ (t²-3) / t ].
Substituting t=3: (3²-3)/3 = (9-3)/3 = 6.
(The provided solution arrives at 36, let's re-check the problem statement)
The denominator is t - 9/t, not t - 3²/t.
lim (t→3) [ (t²-9) (t²-3) / t² ] * [ t / (t-3) (t+3)/t ]
This leads to the same cancellation. Let's re-examine the image's steps.
lim (t-3) (t³ - 27)/ (t-3) . The algebra in the image is hard to follow but seems to manipul
New answer posted
2 months agoContributor-Level 10
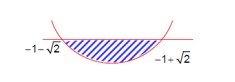
Var (1, 2, ., n) = (Σn²/n) - (Σn/n)² = 10.
(n (n+1) (2n+1)/6n) - (n (n+1)/2n)² = 10.
(n+1) (2n+1)/6 - (n+1)/2)² = 10.
(n+1)/12 * [2 (2n+1) - 3 (n+1)] = 10.
(n+1)/12 * (4n+2 - 3n-3) = 10.
(n+1) (n-1)/12 = 10.
n² - 1 = 120 ⇒ n² = 121 ⇒ n = 11.
Var (2, 4, ., 2m) = Var (2* (1, 2, ., m) = 2² * Var (1, 2, ., m) = 16.
4 * Var (1, 2, ., m) = 16.
Var (1, 2, ., m) = 4.
Using the formula from above: (m²-1)/12 = 4.
m² - 1 = 48 ⇒ m² = 49 ⇒ m = 7.
m + n = 7 + 11 = 18.
New answer posted
2 months agoContributor-Level 9
f (x) + f (x + 1) = 2 (1)
replace x with x + 1: f (x + 1) + f (x + 2) = 2 (2)
(2) - (1) ⇒ f (x + 2) = f (x)
∴ f (x) is periodic with period 2.
I? = ∫? f (x)dx = 4 ∫? ² f (x)dx.
I? = ∫? ³ f (x)dx = ∫? f (u-1)du. Let u = x+1.
I? = ∫? f (x-1)dx = 2 ∫? ² f (x-1)dx.
From (1), f (x-1) + f (x) = 2.
I? + 2I? = 4∫? ² f (x)dx + 2 (2∫? ² f (x-1)dx) = 4∫? ² f (x)dx + 4∫? ² (2 - f (x)dx
= 4∫? ² (f (x) + 2 - f (x)dx = 4∫? ² 2 dx = 4 [2x] from 0 to 2 = 16.
New answer posted
2 months agoContributor-Level 9
y (x) = ∫? (2t² - 15t + 10)dt
dy/dx = 2x² - 15x + 10.
For tangent at (a, b), slope is m = dx/dy = 1 / (dy/dx) = 1 / (2a² - 15a + 10).
Given slope is -1/3.
2a² - 15a + 10 = -3
2a² - 15a + 13 = 0 (The provided solution has 2a²-15a+7=0, suggesting a different problem or a typo)
Following the image: 2a² - 15a + 7 = 0
(2a - 1) (a - 7) = 0
a = 1/2 or a = 7.
a = 1/2 Rejected as a > 1. So a = 7.
b = ∫? (2t² - 15t + 10)dt = [2t³/3 - 15t²/2 + 10t] from 0 to 7.
6b = [4t³ - 45t² + 60t] from 0 to 7 = 4 (7)³ - 45 (7)² + 60 (7) = 1372 - 2205 + 420 = -413.
|a + 6b| = |7 - 413| = |-406| = 406.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 679k Reviews
- 1800k Answers