Maths
Get insights from 6.5k questions on Maths, answered by students, alumni, and experts. You may also ask and answer any question you like about Maths
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
2 months agoContributor-Level 9
Equation of chord of x² + y² = 25 with mid point (h, k) is xh + yk = h² + k².
Or, y = (-h/k)x + (h² + k²)/k.
If this touches the ellipse x²/9 + y²/16 = 1, then the condition for tangency c² = a²m² + b² must be satisfied.
Here, m = -h/k, c = (h²+k²)/k, a²=9, b²=16.
(h² + k²)/k)² = 9 (-h/k)² + 16
(h² + k²)²/k² = 9h²/k² + 16
⇒ (h² + k²)² = 9h² + 16k²
∴ Required locus (x² + y²)² = 9x² + 16y².
New answer posted
2 months agoContributor-Level 10
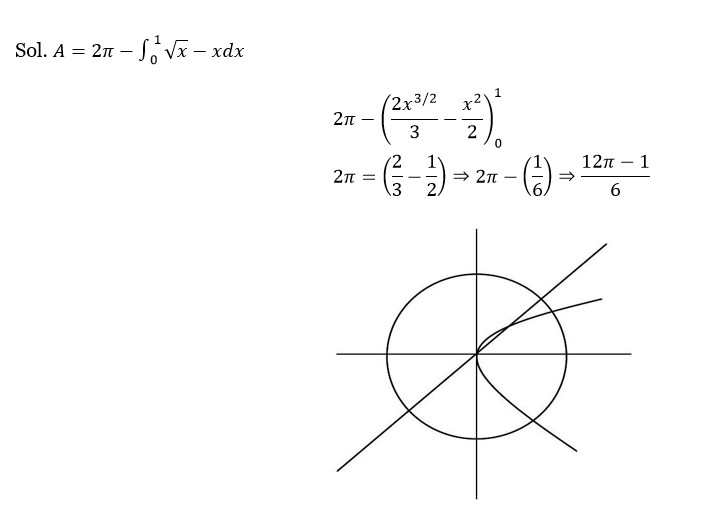
Area A = 2π - ∫? ¹ (√x - x) dx is incorrect. The area is likely between two curves.
The calculation shown is:
A = 2π - [2/3 x^ (3/2) - x²/2] from 0 to 1.
A = 2π - (2/3 - 1/2) = 2π - (4/6 - 3/6) = 2π - 1/6 = (12π - 1)/6.
New answer posted
2 months agoThe number of roots of the equation, (81)sin²? + (81)cos²? = 30 in the interval [0, π] is equal to :
Contributor-Level 9
(81)^sin²x + (81)^cos²x = 30.
(81)^sin²x + (81)^ (1-sin²x) = 30.
Let y = 81^sin²x.
y + 81/y = 30
y² - 30y + 81 = 0
(y - 3) (y - 27) = 0
⇒ y = 3 or y = 27.
Either 81^sin²x = 3 ⇒ 3^ (4sin²x) = 3¹ ⇒ sin²x = 1/4 ⇒ sin x = ±1/2. x = π/6, 5π/6.
OR, 81^sin²x = 27 ⇒ 3^ (4sin²x) = 3³ ⇒ sin²x = 3/4 ⇒ sin x = ±√3/2. x = π/3, 2π/3.
(as 0 ≤ x ≤ π)
Total possible solutions = 4.
New answer posted
2 months agoContributor-Level 9
AC is collinear with l, m, n.
(l/a) = (m/-a) = (n/4) = λ.
Again (0, -a, -1) lies on lx + my + nz = 0.
l (0) + m (-a) + n (-1) = 0 ⇒ -am - n = 0
-a (-aλ) - (4λ) = 0 ⇒ a²λ - 4λ = 0 ⇒ a² = 4, a = ±2.
for a > 0, a = 2. Direction ratios of BD are 2, -2, 4.
Equation of BD: x/2 = (y - 4)/-2 = (z - 5)/4 = r.
Any point on it (2r, 4 - 2r, 5 + 4r) lies on plane lx + my + nz = 2x - 2y + 4z = 0.
⇒ 4r - 2 (4 - 2r) + 4 (5 + 4r) = 0 ⇒ 24r + 12 = 0 ⇒ r = -1/2.
∴ D (-1, 5, 3), C (0, -2, -1).
∴ CD = √ (0 - (-1)² + (-2 - 5)² + (-1 - 3)²) = √ (1 + 49 + 16) = √66
New answer posted
2 months agoContributor-Level 10
For the quadratic equation (k+1)tan²x - √2λ tanx + (k-1) = 0, the roots are tanα and tanβ.
Sum of roots: tanα + tanβ = √2λ / (k+1).
Product of roots: tanα tanβ = (k-1) / (k+1).
tan (α + β) = (tanα + tanβ) / (1 - tanα tanβ)
tan (α + β) = [√2λ / (k+1)] / [1 - (k-1)/ (k+1)]
tan (α + β) = [√2λ / (k+1)] / [ (k+1 - k + 1)/ (k+1)] = (√2λ) / 2 = λ/√2.
Given tan² (α+β) = 50.
(λ/√2)² = 50
λ²/2 = 50 ⇒ λ² = 100 ⇒ λ = ±10.
New answer posted
2 months agoContributor-Level 10
Given kx^ (k-1) + k * y^ (k-1) * dy/dx = 0.
dy/dx = - (kx^ (k-1) / (ky^ (k-1) = - (x/y)^ (k-1).
The provided solution has dy/dx + (x/y)^ (k-1) = 0.
It seems to relate to k-1 = -1/3, which implies k = 1 - 1/3 = 2/3.
New answer posted
2 months agoContributor-Level 10
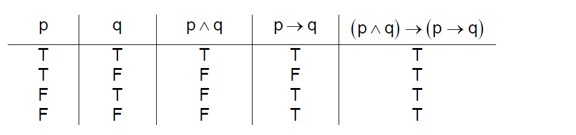
Truth table for (p → q) ∧ (q → ~p).
| p | q | p → q | ~p | q → ~p | (p → q) ∧ (q → ~p) |
|-|-|-|-|-|-|
| T | T | T | F | F | F |
| T | F | F | F | T | F |
| F | T | T | T | T | T |
| F | F | T | T | T | T |
The final column is F, T, which is the truth table for ~p.
Therefore, (p → q) ∧ (q → ~p) is equivalent to ~p.
New answer posted
2 months agoContributor-Level 9
y² - 2x = 4√ (y² - 2x + 1)
Let y² - 2x = k.
k = 4√ (k+1) ⇒ k² = 16 (k+1) ⇒ k²-16k-16=0
(This appears to be from another problem. The provided solution text says:)
y² = 2x = 4 (1/2 x)
a > 2 * (1/2) ⇒ a > 1.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 679k Reviews
- 1800k Answers