Ncert Solutions Maths class 11th
Get insights from 1.6k questions on Ncert Solutions Maths class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Ncert Solutions Maths class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
8 months agoContributor-Level 10
7. i. Let the points be P (0, 7, –10), Q (1, 6, –6) and R (4, 9, –6)
So,
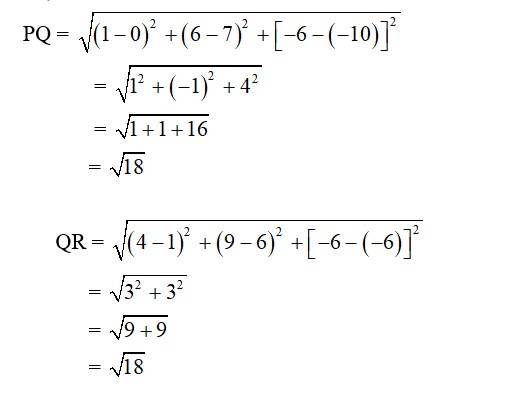




New answer posted
8 months agoContributor-Level 10
6. Here, an=n
Putting n=1,2,3,4,5 we get,
Hence, the first five terms are .
New answer posted
8 months agoContributor-Level 10
3. Here an=2n
Substituting n=1,2,3,4,5 we get,
a1=21=2
a2=22=4
a3=23=8
a4=a4=16
a5=25=32.
Hence the first five terns are 2,4,16,32 and 64.
New answer posted
8 months agoContributor-Level 10
2. Here, a1=
Substituting n=1,2,3,4,5 we get,
.
Hence the first five terns are and .
New answer posted
8 months agoContributor-Level 10
1. Since the ordered pairs are equal, the corresponding elements are equal.
and
y = 1.
New answer posted
9 months agoContributor-Level 10
This is a Mathematical Reasoning Solutions Type Questions as classified in NCERT Exemplar
The given statement can be written in five different ways: –
(i) A triangle is equiangular implies that it is an obtuse angled triangle.
(ii) A triangle is equiangular only if the triangle is an obtuse angled triangle.
(iii) For a triangle to be equiangular, it is necessary that the triangle is an obtuse angled triangle.
(iv) For a triangle to be an obtuse angled triangle, it is sufficient that the triangle is equiangular.
(v) If a triangle is an obtuse angled triangle, then the triangle is not equiangular.
New answer posted
9 months agoContributor-Level 10
This is a Mathematical Reasoning Solutions Type Questions as classified in NCERT Exemplar
(i) The given statement is as follows.
p : the sum of an irrational number and a rational number is irrational.
Let us assume that, p is false.
i.e. The sum of an irrational number and rational number is rational.
Hence, √a where √a is irrational and b, c, d, e are integers.
is a rational number and √a is an irrational number.
This is a contradiction. Therefore, our assumption is wrong.
Therefore, the sum of an irrational number and a rational number is rational.
Thus, the given statement is true.
(ii) The given statement,
New answer posted
9 months agoContributor-Level 10
This is a Mathematical Reasoning Solutions Type Questions as classified in NCERT Exemplar
The compound statement with 'And' is as follows 25 is a multiple of 5 and 8.
This is false statement because 25 is not a multiple of 8.
The compound statement with 'Or' is as follows 25 is a multiple of 5 or 8.
This is true statement because 25 is not a multiple of 8 but it is a multiple of 5.
New answer posted
9 months agoContributor-Level 10
This is a Mathematical Reasoning Solutions Type Questions as classified in NCERT Exemplar
(i) You watch television if and only if your mind is free.
(ii) You get an A grade if and only if you do all the homework regularly.
(iii) A quadrilateral is equiangular if and only if it is a rectangle.
New answer posted
9 months agoContributor-Level 10
This is a Mathematical Reasoning Solutions Type Questions as classified in NCERT Exemplar
(i) The statement p in the form 'if then' is as follows.
If you log on to the server, then you have password.
(ii) The statement q in the form 'if then' is as follows.
If it rains, then there is a traffic jam.
(iii) The statement r in the form 'if them' is as follows.
If you can access the website, then you pay a subscription fee.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 687k Reviews
- 1800k Answers
