Physics Gravitation

Mass of the Earth, M = 6.0 $*{10}^{24}$ kg

Radius of the Earth, R = 6400 km = 6.4 $*{10}^6$ m

Height of geostationary satellite from the surface of the Earth, h = 36000 km = 3.6 $*{10}^7$ m

Gravitational potential energy due to Earth's gravity at height h:

= $\frac{-GM}{(R+h)}$

= $-\frac{6.67*{10}^{-11}*6.0*{10}^{24}}{3.6*{10}^7+6.4*{10}^6}$ = $-\frac{6.67*6.0*{10}^{13}}{4.24*{10}^7}$ = $-$ 9

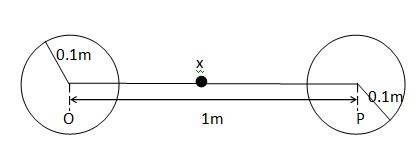
Mass of each sphere, M = 100 kg

Separation between the spheres, r = 1 m

X is the midpoint between the spheres.

Gravitational force at point x will be zero. This is because gravitational force exerted by each spheres will act in opposite directions.

Gravitational potential at point x:

= $\frac{-GM}{\frac{r}{2}}$ $\frac{-GM}{\frac{r}{2}}$ =

Mass of each star, M = 2 × 10³⁰ kg, Radius of each star, R = 10⁴ km = ${10}^7$ m

Distance between stars, r = ${10}^9$ km = ${10}^{12}$ m

For negligible speed, v = 0

The total energy of two stars separated at a distance r

= $-\frac{GMM}{r}+\frac{1}{2}m{v}^2$ = $-\frac{GMM}{r}$ …….(i)

Now, consider the case when the stars are about to co

Mass of the Earth, M = 6.0 × 10²⁴ kg

Mass of the satellite, m = 200 kg

Radius of the Earth, $R_e$ = 6.4 ×10⁶ m

Universal gravitational constant, G = 6.67 × 10^–11 N m² kg^–2

Height of the satellite, h = 400 km = 0.4 $\times {10}^6$ m

Total energy of the satellite at height h = $\frac{1}{2}{mv}^2$ + ( $\frac{-G{M}_{e}m}{R_e+h}$ )

Orbital

Escape velocity of the projectile on the Earth’s surface, $v_{esc}$ = 11.2 km/s = 11.2 ${\times 10}^3$ m/s

Projection velocity of the projectile = 3 $v_{esc}$

Mass of the projectile = m

Velocity of the projectile far away from the Earth = $v_f$

Total energy of the projectile on the Earth = $\frac{1}{2}$ m ${v_p}^2$&nb

Velocity of the rocket, v = 5 km/s = 5 $\times {10}^3$ m/s

Mass of the Earth, $M_e$ = 6.0 × 10²⁴ kg

Radius of the Earth, $R_e$ = 6.4 × 10⁶ m

Height reached by rocket mass, m = h

At the Earth’s surface

Total energy of the rocket = Kinetic energy + Potential energy = $\frac{1}{2}$ m $v^2$ + ( $\frac{-G{mM}_e}{R_e}$ )

At h

Weight of a body of mass m at Earth's surface, W = mg = 250 N

Body of mass m is located at depth, d = $\frac{1}{2}{R}_e$ , where $R_e$ is radius of the Earth

Acceleration due to gravity at depth g (d) is given by : g' = (1 - $\frac{d}{R_e}$ )g = (1/2)g

Weight of the body at depth d

W' = mg' = (1/2) mg = (1/2)W

Weight of the body, W = 63 N

Acceleration due to gravity at h from the Earth's surface is given by

g' = $\frac{g}{{\left(\frac{1+h}{R_e}\right)}^2}$ where g = acceleration due to gravity on the Earth's surface,  $R_e$ = Radius of the Earth. h = $\frac{R_e}{2}$

g' = $\frac{g}{{\left(\frac{1+R_e/2}{R_e}\right)}^2}$ = $\frac{g}{{\left(\frac{1+h}{2h}\right)}^2}$ = (4/9)g

Weight of the body of mass m at a height h i

Distance of the Earth from the Sun, $r_e$ = 1.50 × 10⁸ km = 1.5 × 10¹¹ m

Time period of the Earth = $T_e$ , Time period of the Saturn $T_s$ = ${29.5T}_e$

Distance of Saturn from the Sun = $r_s$

From Kepler’s 3rd law of planetary motion, we have T =( ${\frac{4{\pi }^2{r}^3}{GM})}^{1/2}$

For Saturn and Sun, we can write, $\frac{r_s^3}{r_e^3}$ 

Orbital radius of the Earth around the Sun, r = 1.5 × 10⁸ km = 1.5 × 10¹¹ m

Time taken by the Earth to complete 1 revolution around the Sun, T = 1 year = 365.25 days = 365.25 $\times$ 24 $\times 24\times 60\times 60s$

Universal gravitational constant, G = 6.67 $\times {10}^{-11}$ N $m^2/{kg}^2$

Thus, mass of the Sun can be calculated as,

M