Physics Gravitation

$g^1=g\left(1-\frac{2h}{R}\right)=g\left(1-2*\frac{32}{6400}\right)$

$g^1=\frac{99g}{100}=0.99g$

% decrease is wt = $\frac{g-g^1}{g}*100=1\mathrm{\%}$

$g^{\prime }=\frac{G{M}^{\prime }}{R^{\text{'}2}}=\frac{GM}{10{\left(\frac{R}{2}\right)}^2}$

$=\frac{4}{10}\frac{GM}{R^2}=0.4*9.8$

$=3.92 m s^{-2}$

Using conservation of energy :

$?\frac{?GMm}{R}+\frac{1}{2}m{\left(\sqrt[]{\frac{2GM}{R}}\right)}^2=\frac{?GMm}{r}+\frac{1}{2}m{v}^2$

$?\frac{1}{2}m{v}^2=\frac{GMm}{r}$

$?{\displaystyle \underset{R}{\overset{R+h}{?}}{r}^{1/2}dr=\sqrt[]{2GM}{\displaystyle \underset{0}{\overset{t}{?}}dt}}$

$?\frac{2}{3}{R}^{3/2}\left[{\left(1+\frac{h}{R}\right)}^{3/2}?1\right]=\sqrt[]{2GM}t$

$t=\frac{1}{3}\sqrt[]{\frac{2R}{g}}\left[{\left(1+\frac{h}{R}\right)}^{3/2}?1\right]$

W₁ = 1000 N ->Weight of person at surface of earth W₂ = 400 N Þ Weight of person at surface of Mars. There will be a neutral point -N where weight will be zero because at this point net gravitational field due to earth and mars is zero.

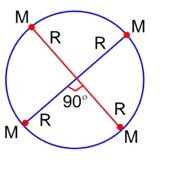
Since binary mass system performs circular motion about is common centre of mass, so

$m_A{\omega }_A^2{r}_A=\frac{G{m}_B{m}_A}{{\left(r_A+r_B\right)}^2}=\frac{G{m}_B{m}_A}{r^2}$

$m_A{\omega }_A^2*\frac{m_B}{\left(m_A+m_B\right)}r=\frac{G{m}_B{m}_A}{r^2}$

${\omega }_A=\sqrt[]{\frac{G\left(m_A+m_B\right)}{r^3}}$

Similarly we can show that

${\omega }_B=\sqrt[]{\frac{G\left(m_A+m_B\right)}{r^3}}$

Hence their angular velocity will be same, time period will be same, i.e. TA = TB

Time period of Satellite = T = $\frac{2\pi R}{v}={\left(\frac{4{\pi }^2{R}^3}{GM}\right)}^{\frac{1}{2}}$  

$\Rightarrow T\alpha R^{\frac{3}{2}}\Rightarrow \frac{T_2}{T_1}=\frac{{\left(1.02R\right)}^{\frac{3}{2}}}{R^{\frac{3}{2}}}={\left(1.02\right)}^{\frac{3}{2}}={\left(1+0.02\right)}^{\frac{3}{2}}$     

The percentage difference in the time periods of the two satellites = $\frac{\Delta T}{T_1}$ * 100

= (0.03) * 100 = 3%

For circular motion F_{net   $=\frac{M{V}^2}{R}$}

_{$\sqrt[]{2F}+F\text{'}=\frac{M{V}^2}{R}$}

$\sqrt[]{2}\frac{GMM}{{\left(\sqrt[]{2}R\right)}^2}+\frac{GMM}{{\left(2R\right)}^2}=\frac{M{V}^2}{R}$                

$\frac{GM}{R}\left[\frac{1}{\sqrt[]{2}}+\frac{1}{4}\right]=V^2$              

$V=\frac{1}{2}\sqrt[]{\frac{GM}{R}\left(2\sqrt[]{2}+1\right)}$

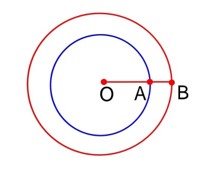
For A satellite T₁ = 1hour

$So{\omega }_1=2\pi red/hour$                

for B satellite T₂ = 8 hour

given R₁ = 2 * 10³ Km

Relative  $\omega =\frac{V_1-V_2}{R_2-R_1}=\frac{2\pi *10^3}{6*10^3}$  

$\Rightarrow \frac{\pi }{3}$ rad/hour

 x = 3

For circular motion F_{net   $=\frac{M{V}^2}{R}$}

_{$\sqrt[]{2F}+F\text{'}=\frac{M{V}^2}{R}$}

$\sqrt[]{2}\frac{GMM}{{\left(\sqrt[]{2}R\right)}^2}+\frac{GMM}{{\left(2R\right)}^2}=\frac{M{V}^2}{R}$                

$\frac{GM}{R}\left[\frac{1}{\sqrt[]{2}}+\frac{1}{4}\right]=V^2$              

$V=\frac{1}{2}\sqrt[]{\frac{GM}{R}\left(2\sqrt[]{2}+1\right)}$

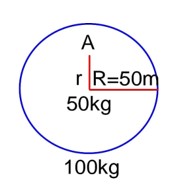
Acceleration due to gravity at r distance above the surface = $\frac{GM}{{\left(R+r\right)}^2}$  

Acceleration due to gravity at r distance below the surface = $\frac{GM}{R^3}\left(R-r\right)$

So, ratio = $\frac{\left(R-r\right){\left(R+r\right)}^2}{R^3}=\frac{\left(R-r\right)\left(R^2+r^2+2Rr\right)}{R^3}=1+\frac{r}{R}-\frac{r^2}{R^2}-\frac{r^3}{R^3}$