Physics System of Particles and Rotational Motion
Get insights from 151 questions on Physics System of Particles and Rotational Motion, answered by students, alumni, and experts. You may also ask and answer any question you like about Physics System of Particles and Rotational Motion
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
3 months agoContributor-Level 9
Statement (1) is correct
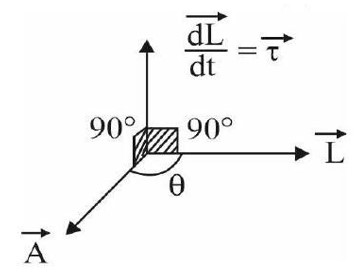
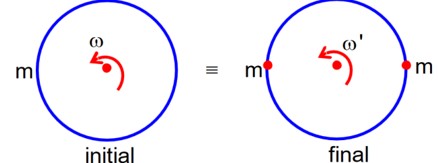
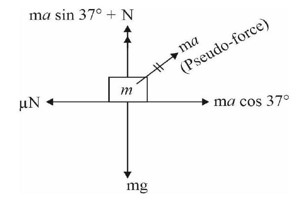
The component of in the direction of is always perpendicular to , so it does not change.
Statement (2) is correct
The magnitude of does not change with time as .
Statement (3) is correct
The direction of changes with time.
Statement (4) is incorrect.
New answer posted
3 months agoContributor-Level 10
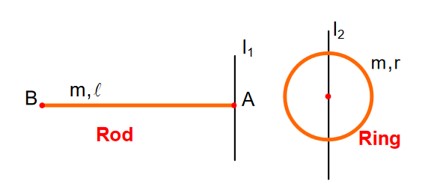
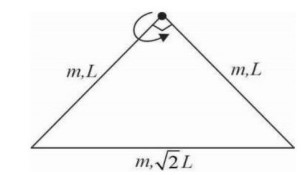
L = Iω
I = (mL²/3) + (mL²/3) + [m (√2L)²/12] + m (L/√2)² = mL² [2/3 + 1/6 + 1/2] = (4mL²/3); L = (4/3)mL²ω
New answer posted
3 months agoContributor-Level 10
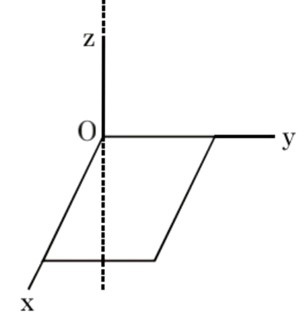
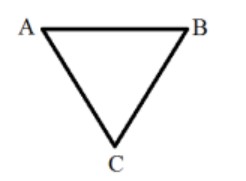
Using parallel axis theorem for the side BC, the moment of inertia of the triangle about an axis passing through A and perpendicular to the plane of the triangle,
I? = 2 [ (1/3)ma²] + [ (1/12)ma² + m (√3a/2)²] = (3/2)ma²
If the angular velocity of the triangle at any instant is ω, the velocity of the vertex B at that instant is aω
Therefore, the velocity of B is maximum at the instant the angular velocity is maximum, i.e. when the side BC becomes horizontal
Let the angular velocity at this instant be ω?
Then, by conservation of energy
Gain in kinetic energy = Loss in potential energy
(1/2)I? ω²? = 3mg (Loss in height of CM of tr
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 680k Reviews
- 1800k Answers