Physics System of Particles and Rotational Motion
Get insights from 151 questions on Physics System of Particles and Rotational Motion, answered by students, alumni, and experts. You may also ask and answer any question you like about Physics System of Particles and Rotational Motion
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
3 months agoContributor-Level 10
Even if the torque is same, the rotation of a body can be slow or fast depending on the distribution of mass along the surface area. If the mass of a body is more on the axis area, it's speed of rotation will be faster as compared to the body whose mass is accumulated away from the axis due to which the body will resist the angular acceleration.
New answer posted
3 months agoContributor-Level 10
In simple words, a push or pull applied on a body is known as a force. Force is a concept used in terms of linear motion. On the other hand, the force which causes a body to spin around an axis instead of moving from one point to aother is called torque. Torque is a theory which comes into account while studying rotational motion and is considered as the rotational analogue of force.
New answer posted
3 months agoContributor-Level 10

Let the gravitational field is zero at a distance from the mass .
or
Gravitational potential at ![]()
New answer posted
3 months agoContributor-Level 10
Radius of gyration of a solid surface,
Radius of gyration of a hollow surface,
New answer posted
3 months agoContributor-Level 10
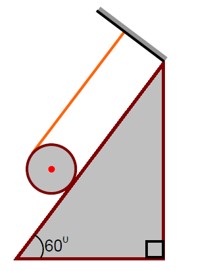
μ_min = (I tanθ)/ (I + mR²)
= [ (mR²/2)tanθ] / [mR²/2 + mR²] = (tanθ)/3 = (tan 60°)/3 = √3/3 = 1.732/3 = 0.5773
Since given coefficient of static friction is less than μ_min, so body will perform rolling with slipping and kinetic friction will act
F? = μN = μmg cosθ = (0.4) * mg cos 60° = mg/5
New question posted
3 months agoNew answer posted
3 months agoContributor-Level 10
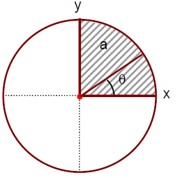
The x and y coordinates of the center of mass are given by:
x? = y? = 4a / 3π
New answer posted
3 months agoContributor-Level 9
Using conservation of Angular momentum along axis of rotation, we can write
Mr²ω = (Mr² + 2mr²)ω? ⇒ ω? = Mω / (M + 2m)
New answer posted
3 months agoContributor-Level 10
The number of revolutions can be found using the rotational kinematic equation for angular displacement (θ):
θ = (ω_initial + ω_final)/2 * t
Number of revolutions = θ / 2π
Number of revolutions = [ (ω_final + ω_initial) * t] / (2 * 2π)
Based on the numerical values provided in the document, the calculation is:
Number of revolution = [ (2π * 3360/60 + 0) * t] / (2 * 2π) . with further calculation yielding the result:
Number of revolution = 728
New answer posted
3 months agoContributor-Level 10
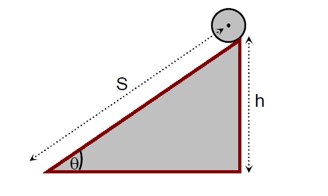
The equations for an object rolling down an inclined plane without slipping are:
· Force equation: mg sinθ - f_s = ma
· Torque equation: f_s R = Iα
Since a = αR, we can write f_s = Iα/R = Ia/R².
Substituting this into the force equation:
mg sinθ - Ia/R² = ma
mg sinθ = a (m + I/R²)
a = (mg sinθ) / (m + I/R²)
The time taken to travel a distance S is given by S = ½ at², which means t ∝ 1/√a. Therefore, the object with the largest acceleration (a) will arrive first.
The problem is analyzed for different bodies:
· Ring: I =
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 680k Reviews
- 1800k Answers