Physics Waves
Get insights from 104 questions on Physics Waves, answered by students, alumni, and experts. You may also ask and answer any question you like about Physics Waves
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
Frequency of the whistle, = 400 Hz
Speed of the train, = 10 m/s
Speed of sound, v = 340 m/s
The apparent frequency (f') of the whistle as the train approaches the platform is given by the relation:
f' = ( = ( 412.12 Hz
The apparent frequency (f”) of the whistle as the train recedes from the platform is given by the relation:
f” = ( = ( 388.57 Hz
The apparent change in the frequency of sound is caused by the relative motions of the source and the observer. These relative motions produce no effect on the speed of sound.
Therefore, the speed of sound in air in both the cases
New answer posted
7 months agoContributor-Level 10
(a) A node is a point where the amplitude of vibration is the minimum and the pressure is maximum. On the other hand, an antinode is a point where the amplitude of vibration is maximum and the pressure is minimum. Therefore, a displacement node is nothing but a pressure antinode and vice versa.
(b) Bats emit very high-frequency ultrasonic sound waves. These waves get reflected back toward them by obstacles. A bat receives a reflected wave (frequency) and estimates the distance, direction, nature and size of the obstacle with the help of its brain senses.
(c) The overtone produced by a sitar and a violin, and the strengths
New answer posted
7 months agoContributor-Level 10
Frequency of string A, = 324 Hz, let the frequency of string B, be =
Beat's frequency, n = 6 Hz
Beat's frequency is given as n = or 6 = 324
Frequency decreases with a decrease in the tension in a string. This is because frequency is directly proportional to the square root of tension, . It is given as
Hence the beat frequency cannot be 330 Hz. So
New answer posted
7 months agoContributor-Level 10
Length of the pipe, l = 20 cm = 0.2 m
Source frequency = normal mode frequency is given by the relation
= (2n-1) , n is an integer = 0,1,2,3, ….
430 = (2n-1)
n = 1
Hence, the first mode of vibration frequency is resonantly excited by the given source. In a pipe open at both ends, the mode of vibration frequency is given by the relation:
, n = = = 0.5
Since the number of the node of vibration (n) has to be an integer, the given source does not produce a resound vibration in an open pipe.
New answer posted
7 months agoContributor-Level 10
Length of the steel rod, l = 100 cm = 1 m
Fundamental frequency of vibration, = 2.53 kHz = 2.53 Hz
When the rod is plucked at its middle, an antinode (A) is formed at the centre, and the nodes (N) are formed at its two ends, as shown in the figure.
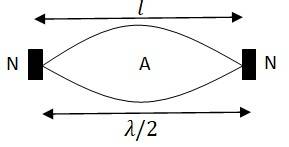
The distance between two successive nodes is
l = = 2l = 2 m
The speed of sound in steel is given by the relation
v = = 2.53 = 5.06 m/s = 5.06 km/s
New answer posted
7 months agoContributor-Level 10
Frequency of the tuning fork, = 340 Hz
Since the given pipe is attached with a piston at one end, it will behave as a pipe with one end closed and the other end open, as shown in this figure.
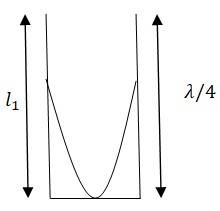
= of the pipe = 25.5 cm = 0.255 m
= 4 m = 1.02 m
The speed of sound is given by the relation, v = = 340 = 346.8 m/s
New answer posted
7 months agoContributor-Level 10
Mass of the wire, m = 3.5 kg
Linear mass density, = 4 kg/m
Frequency of vibration, = 45 Hz
Length of the wire, l = = = 0.875 m
The wavelength of the stationary wave = , where n = number of nodes in the wire
For fundamental node, n = 1, = 2l = 2
(a) The speed of the transverse wave in the string is given as v = = 45 = 78.75 m/s
(b) The tension produced in the string is given by the relation, T = = 4 = 248.06 N
New answer posted
7 months agoContributor-Level 10
(a) The given equation represents a stationary wave because the harmonic terms kx and appear separately in the equation.
(b) The given equation does not contain any harmonic term. Therefore, it does not represent either a travelling wave or a stationary wave.
(c) The given equation represents a travelling wave as the harmonic terms kx and are in the combination of kx – .
(d) The given equation represents a stationary wave because the harmonic terms kx and in the equation. This equation represents the superposition of two stationary waves.
New answer posted
7 months agoContributor-Level 10
(i)
(a) All the points on the string oscillates with the same frequency, except at the nodes, which have zero frequency
(b) All the points in any vibrating loop have the same phase, except at the nodes.
(c) All the points in any vibrating loop will have different amplitudes of vibration.
(ii)
The given equation is: y (x, t) = 0.06 sin ( cos (120
For x = 0.375 and t =0
Amplitude = Displacement = 0.06 sin ( cos (0 = 0.06sin ( = 0.042 m
New answer posted
7 months agoContributor-Level 10
(a) The general equation representing a stationary wave is given by the displacement function y(x,t) = 2asin kx cos
The equation is similar to the give equation y(x, t) = 0.06 sin ( cos (120
Hence, the given function represents a stationary wave.
A wave travelling along the positive x-direction is given as: = asin ( t – kx)
The wave travelling along the negative x-direction is given as: = asin ( t + kx)
(b) The superposition of these two waves yields:
y = = asin ( t – kx) + asin ( t + kx)
= a sin( t)cos(kx) – a sin(kx)cos(&nbs
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 680k Reviews
- 1800k Answers
