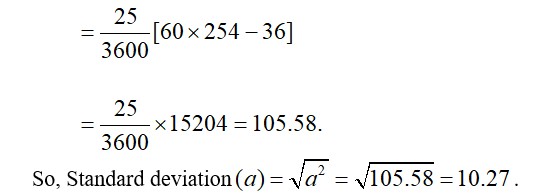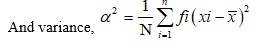Statistics
Get insights from 124 questions on Statistics, answered by students, alumni, and experts. You may also ask and answer any question you like about Statistics
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
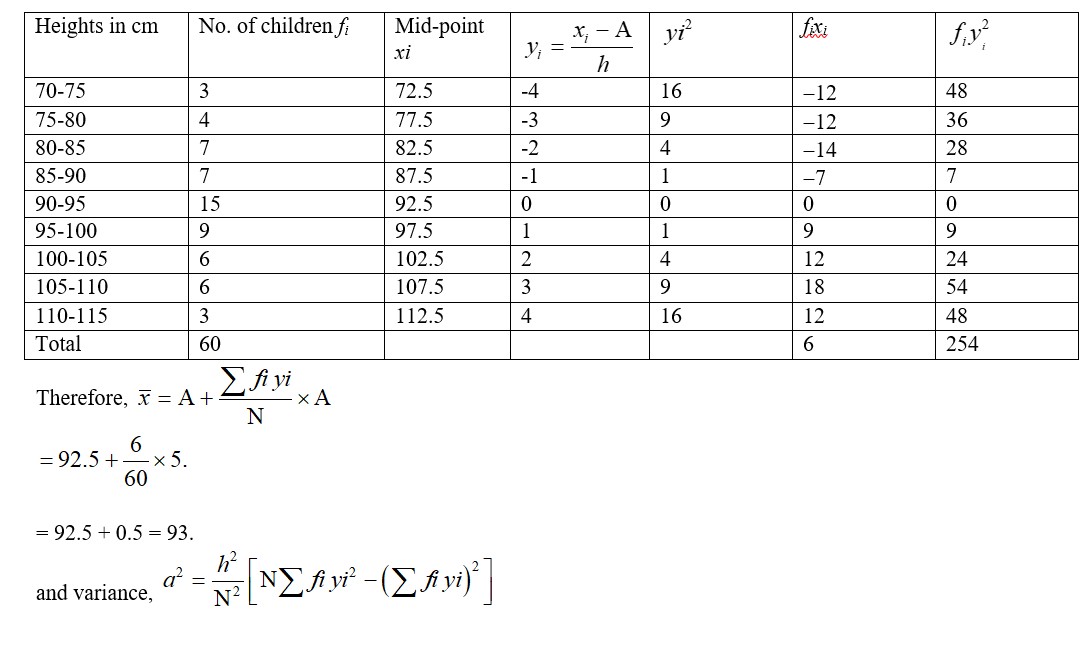
23. Let the assumed mean be A=45 and h=10. Then we can tabulate the given data as following.
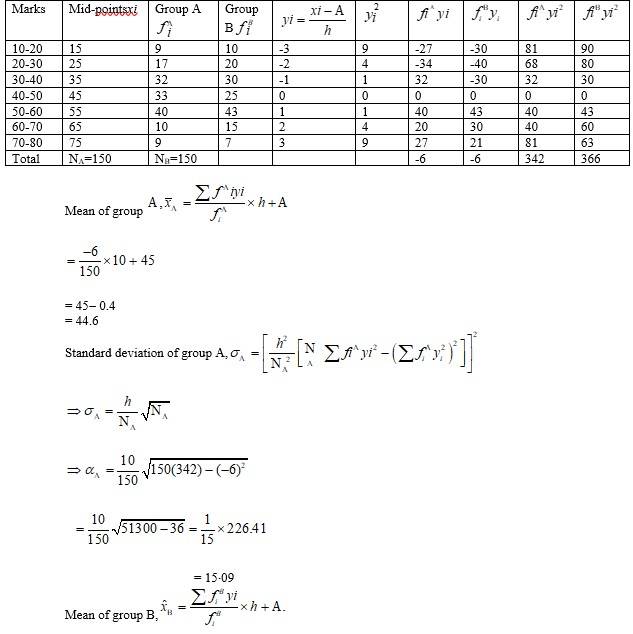
= 44.6
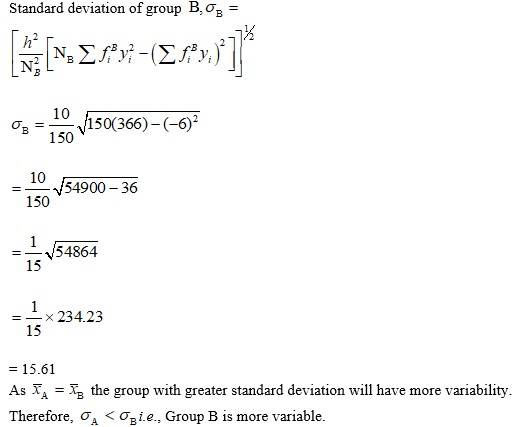
New question posted
7 months agoNew answer posted
7 months agoContributor-Level 10
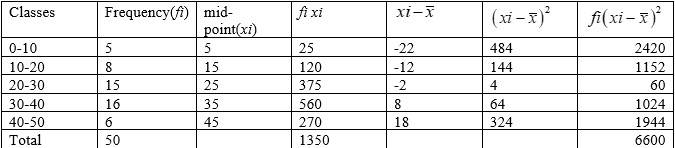
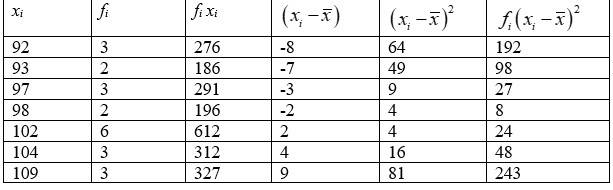
22. The given data is converted into continuous frequency duration by subtracting and adding 0.5 from lower and upper limit respectively. Lit the assumed mean be A=42.5 and h=4
New answer posted
7 months agoContributor-Level 10
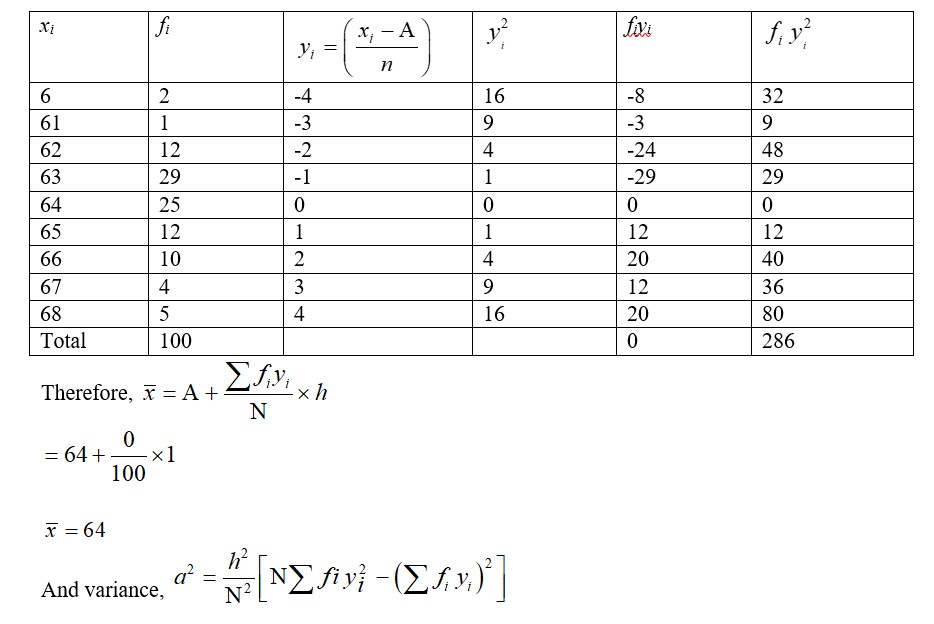
19. Let the assumed mean be A=105 and class width, h=30. The given data can be tabulated as
= 2280 - 4
= 2276.
New question posted
7 months agoTaking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers