Straight Lines
Get insights from 177 questions on Straight Lines, answered by students, alumni, and experts. You may also ask and answer any question you like about Straight Lines
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
3 months agoContributor-Level 9
Slope of AH = slope of BC =
slope of HC =
slope of BC * slope of HC = -1 Þ p = 3 or 5
hence p = 3 is only possible value.
New answer posted
3 months agoContributor-Level 9
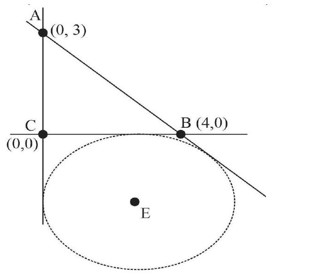
Let point P : (h, k)
Therefore according to question,
locus of P(h, k) is
Now intersection with x – axis are
Now intersection with y – axis are
Therefore are of the quadrilateral ABCD is =
New answer posted
3 months agoContributor-Level 10
If the two lines are perpendicular then a = 2
D = 0
(D = abc + 2fgh - af2 – bg2 - ch2)
New answer posted
3 months agoContributor-Level 10
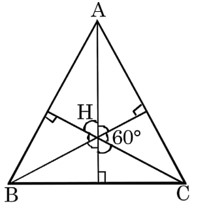
The two altitudes are
Point of int. of the 2 altitudes is
Let slope of 3rd altitude be 'm'
then
The third altitude is x = 2
New answer posted
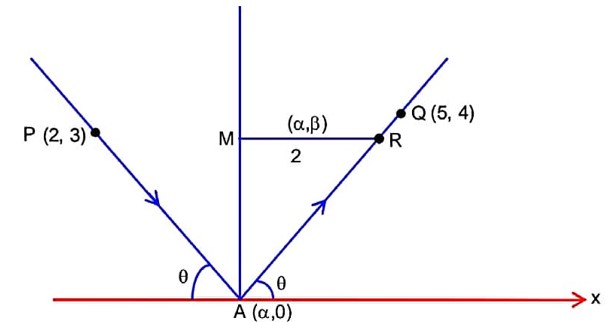
3 months agoContributor-Level 10
(k-3)/ (h-2) * (k-0)/ (h-0) = -1
⇒ k (2k – 3) = -2 (h – 2)h
⇒ 2h² + 2k² – 4h – 3k = 0
2x² + 2y² – 4x – 3y = 0
(0,0)
New answer posted
4 months agoContributor-Level 10
According to question,
Equation of required line is
Obviously B (2, 2) satisfying condition (i)
New answer posted
4 months agoContributor-Level 10
3x² + 3x²y - 3xy² + dy³ = 0
3x² (x + y) – 3y² (x - dy/3) = 0
x - dy/3 = x + y for getting two perpendicular straight lines
d = -3
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers