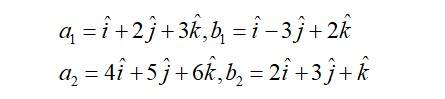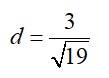Three Dimensional Geometry
Get insights from 212 questions on Three Dimensional Geometry, answered by students, alumni, and experts. You may also ask and answer any question you like about Three Dimensional Geometry
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
Dividing both sides of equation (1) by 5, we obtain
It is known that the equation of a plane in intercept form is , where a, b, c are the intercepts cut off by the plane at x, y, and z axes respectively.
Therefore, for the given equation,
Thus, the intercepts cut off by the plane are
New answer posted
7 months agoContributor-Level 10
We know that through three collinear points i.e., through a straight line, we can pass an infinite number of planes.
(a) The given points are
Since are collinear points, there will be infinite number of planes passing through the given points.
(b) The given points are
Therefore, a plane will pass through the points A, B, and C.
It is known that the equation of the plane through the points, , is
This is the Cartesian equation of the required plane.
New answer posted
7 months agoContributor-Level 10
(a) The position vector of point is
The normal vector N perpendicular to the plane is
The vector equation of the plane is given by,
is the position vector of any point in the plane.
Therefore, equation (1) becomes
This is the Cartesian equation of the required plane.
(b) The position vector of the point is
The normal vector perpendicular to the plane is
The vector equation of the plane is given by,
is the position vector of any point in the plane.
Therefore, equation (1) becomes
This is the Car
New answer posted
7 months agoContributor-Level 10
(a) Let the coordinates of the foot of perpendicular P from the origin to the plane be


New answer posted
7 months agoContributor-Level 10
(a) It is given that equation of the plane is
For any arbitrary point on the plane, position vector I s given by,
Substituting the value of in equation (1), we obtain
This is the Cartesian equation of the plane.
(b)
For any arbitrary point on the plane, position vector is given by,
Substituting the value of in equation (1), we obtain
This is the Cartesian equation of the plane.
(c)
For any arbitrary point on the plane, position vector is given by,
Substituting the value
New answer posted
7 months agoContributor-Level 10
(a) It is given that equation of the plane is
For any arbitrary point on the plane, position vector I s given by,
Substituting the value of in equation (1), we obtain
This is the Cartesian equation of the plane.
(b)
For any arbitrary point on the plane, position vector is given by,
Substituting the value of in equation (1), we obtain
This is the Cartesian equation of the plane.
(c)
For any arbitrary point on the plane, position vector is given by,
Substituting the value
New answer posted
7 months agoContributor-Level 10
(a) The equation of the plane is
The direction ratios of normal are
Dividing both sides of equation (1) by 1, we obtain
This is of the form , where l, m, n are the direction cosines of normal to the plane and d is the distance of the perpendicular drawn from the origin.
Therefore, the direction cosines are 0, 0, and 1 and the distance of the plane from the origin is 2 units.
(b)
The direction ratios of normal are 1, 1, and 1.
Dividing both sides of equation (1) by , we obtain
This equation is of the form , where l, m, n
New answer posted
7 months agoNew answer posted
7 months agoContributor-Level 10
Shortest distance between two lines is given by,

Then,

Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers