Class 12th
Get insights from 12k questions on Class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
4 months agoContributor-Level 10
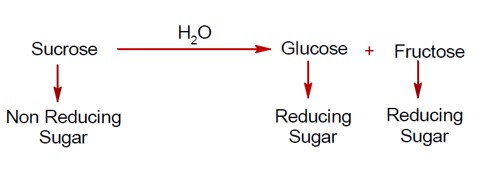
Inversion of Sucrose:
C? H? O? (Sucrose) + H? O - (Invertase)-> C? H? O? (Glucose) + C? H? O? (Fructose)
Fermentation of Glucose:
C? H? O? (Glucose) - (Zymase)-> 2C? H? OH (Ethanol) + 2CO?
New answer posted
4 months agoContributor-Level 10
KMnO? oxidizes alkanes that contain a tertiary hydrogen (3°H) to form tertiary alcohols.
n-alkanes, which do not contain tertiary hydrogens, are not oxidized by KMnO? under these conditions.
New answer posted
4 months agoContributor-Level 10
Evaluate the integral:
∫ (2x-1)cos (√ (4x²-4x+6) / √ (4x²-4x+6) dx
∫ (2x-1)cos (√ (2x-1)²+5) / √ (2x-1)²+5) dx
Let (2x-1)² + 5 = t².
Differentiating both sides:
2 (2x-1)*2 dx = 2t dt
2 (2x-1) dx = t dt
(2x-1) dx = (t/2) dt
Substitute into the integral:
∫ cos (t)/t * (t/2) dt
= 1/2 ∫ cos (t) dt
= 1/2 sin (t) + C
= 1/2 sin (√ (2x-1)²+5) + C
= 1/2 sin (√ (4x²-4x+6) + C
New answer posted
4 months agoContributor-Level 10
Co (NH? )? ] [Cr (CN)? ]: Co-ordination isomerism
[Co (NH? )? (NO? )? ]: Linkage isomerism
[Cr (H? O)? ]Cl? : Solvate isomerism
Cis- [CrCl? (Ox)? ]³? : Optical isomerism
New answer posted
4 months agoContributor-Level 10
The change in entropy for the following processes is negative (ΔS = -ve), indicating an increase in order:
Water (l) → Ice (s) at 0°C
H? O (l) → Ice (s) at -10°C
N? (g) + 3H? (g) → 2NH? (g)
Adsorption
New answer posted
4 months agoContributor-Level 10
Given equations:
3x + 4y = 9
y = mx + 1 (assuming this from the substitution)
Substitute y into the first equation:
3x + 4 (mx + 1) = 9
3x + 4mx + 4 = 9
x (3 + 4m) = 5
x = 5 / (3 + 4m)
For x to be an integer, (3 + 4m) must be a divisor of 5, i.e., ±1, ±5.
- 3 + 4m = 1 => 4m = -2 => m = -1/2
- 3 + 4m = -1 => 4m = -4 => m = -1 (Integer value)
- 3 + 4m = 5 => 4m = 2 => m = 1/2
- 3 + 4m = -5 => 4m = -8 => m = -2 (Integer value)
The two integral values for m are -1 and -2.
New answer posted
4 months agoContributor-Level 10
The reaction shown is:
Anisole diazonium chloride (A) + Ethanol → Anisole + Acetaldehyde (X) + HCl + N? (Y)
New answer posted
4 months agoContributor-Level 10
f (x) + g (x) = √x + √1-x. The domain requires x ≥ 0 and 1-x ≥ 0, so x ≤ 1. Domain is [0,1].
f (x) - g (x) = √x - √1-x. Domain is [0,1].
f (x)/g (x) = √x / √1-x. Requires x ≥ 0 and 1-x > 0, so x < 1. Domain is [0,1).
g (x)/f (x) = √1-x / √x. Requires 1-x ≥ 0 and x > 0. Domain is (0,1].
The common domain for all these functional forms to be considered is (0,1).
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers