Chemical kinetics is the study of the speed of reaction. While thermodynamics tells us whether a reaction can happen, kinetics tells us how fast it actually happens. Let me explain it with an example, diamond turning into graphite - thermodynamics says it should happen, but chemical kinetics in chemistry explains, this process is incredibly slow, which is why we never see it in our lifetime.
Chemical Kinetics class 12 covers various topics such as factors affecting the rate of reaction, temperature dependence, collision theory, etc. To simplify the NCERT chapter, we’ve created Chemical Kinetics class 12 notes, which cover all the important topics and formulas simply and concisely, helping students to revise the chapter quickly and score well in the CBSE board exams.
With the help of chemical kinetics short notes, you will be able to define the average and instant rate of reaction, differentiate between complex and elementary reactions, define the rate constant, and understand how the rate of reaction depends on temperature, concentration, and catalyst.
- What is Chemical Kinetics?
- Rate of a Chemical Reaction
- Factors Affecting Rate of a Reaction
- Integrated Rate Equations
- Temperature Dependence of the Rate of a Reaction
- Collision Theory of Chemical Reactions
- Chemical Kinetics Formulas
- Revision Notes for Class 12 Chemistry
- NCERT Solutions for Class 12 Chemistry
- Chemical Kinetics FAQs
What is Chemical Kinetics?
Rate of a Chemical Reaction
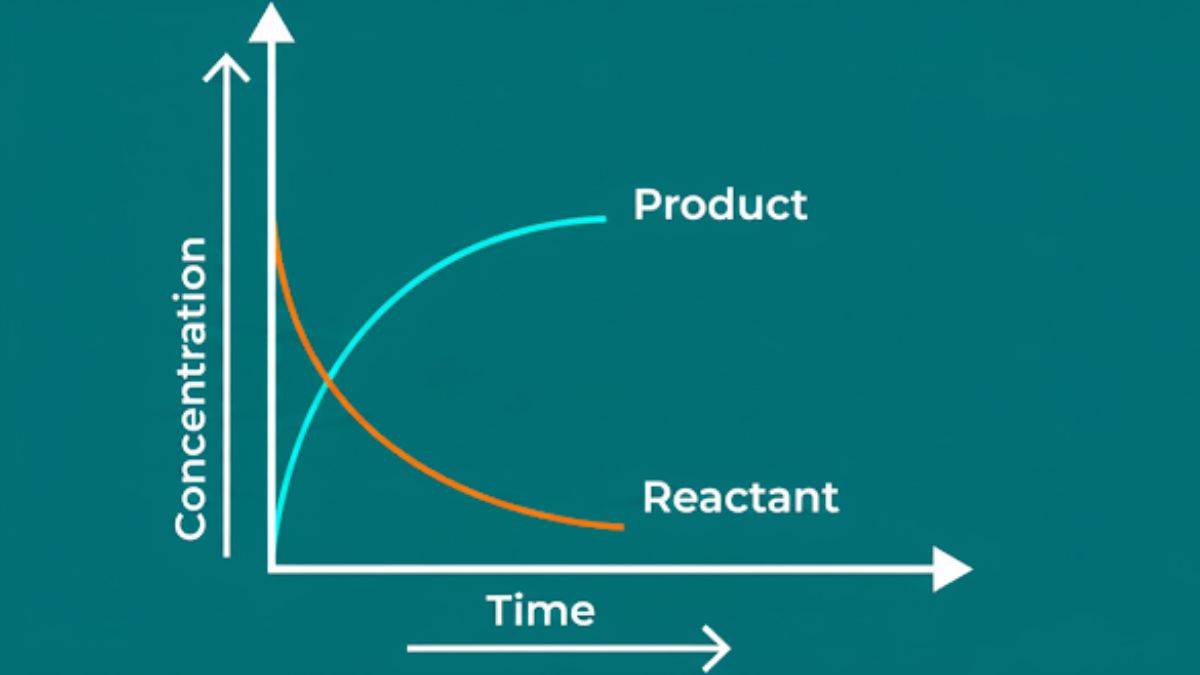
The rate of a chemical reaction or the speed of reaction is defined as how much concentration change in a specific time period. Essentially how fast reactants disappear or how quickly products appear. Just like we measure the speed of a car by how much distance it covers in a given time, we measure reaction rate by.
Average and Instantaneous Rate
When chemical reactions take place, they keep changing speed, and usually the speed of the reaction slows down as reactants are used up. So, there are two types of rate of reaction- Average Rate and Instantaneous Rate.
Average Rate
The average rate of reaction is the speed at which the reaction occurs in the given time.
For a reaction R → P:
- Rate of disappearance of R = -Δ[R]/Δt
- Rate of appearance of P = +Δ[P]/Δt
The negative sign ensures that the rate is always positive, even though the reactant concentration decreases.
Instantaneous Rate
Instantaneous Rate gives the exact rate (speed of a reaction) at a particular instant. It's like checking your speedometer at a specific moment.
- r_inst = -d[R]/dt = +d[P]/dt
This is found by drawing a tangent to the concentration-time curve at the desired point and calculating its slope.
Units of Reaction Rate
The units of rate depend on how we present concentration:
- For molarity: mol L⁻¹ s⁻¹ or M s⁻¹
- For gaseous reactions: atm s⁻¹ or bar s⁻¹
Factors Affecting Rate of a Reaction
Several factors can affect how fast or slow a chemical reaction proceeds. These factors help us control reactions in different settings. Some of the factors affecting the rate of reactions are: concentration of the reactant, temperature, and catalyst.
Dependence of Rate on Concentration
Most reactions speed up when we increase the concentration of reactants. More molecules in a given space means more frequent collisions and faster reactions.
Rate Law
The mathematical relationship between the rate of reaction and concentration is called the rate law or rate expression.
For a general reaction: aA + bB → products
Rate law: Rate = k[A]ˣ[B]ʸ
-d[R]/dt = k[A]ˣ[B]ʸ (this form of the rate law equation is known as the differential rate equation)
Where,
- k = rate constant (specific for each reaction at a given temperature)
- x, y = orders with respect to A and B, respectively
The exponents x and y are not necessarily equal to the stoichiometric coefficients a and b. They must be determined experimentally.
The differential rate equation relates the speed of reaction to the concentration of the reactant, which is known as the rate law.
Order of a Reaction
The order indicates how sensitive the reaction rate (speed of reaction) is to concentration changes. It’s the sum of all exponents in the rate law.
In the rate law,
Rate = k[A]ˣ[B]ʸ
- x and y are the orders of reaction
- Change in concentration will be in the A and B
- x + y = overall order of reaction
Types of orders:
- Zero order: Rate independent of reactant concentration
- First order: Rate directly proportional to [reactant]
- Second order: Rate proportional to [reactant]²
- Fractional order: Possible in complex reactions
Elementary Reaction- when a reaction occurs in a single step without involving any intermediate to form a product. There are three types of elementary reactions: Unimolecular, Bimolecular, and Termolecular.
Complex Reaction- when a reaction occurs in multiple steps with intermediates involved. Each step in a complex reaction is an elementary reaction.
Molecularity of a Reaction
Molecularity refers to the number of molecules that actually participate in an elementary reaction step.
Difference between Order and Molecularity:
| Order |
Molecularity |
| Experimental quantity |
Theoretical concept |
| Can be zero or fractional |
Always a positive integer |
| Applies to the overall reaction |
Only for elementary reactions |
| Determined from the rate law |
Determined from the reaction mechanism |
Examples:
- Unimolecular: NH₄NO₂ → N₂ + 2H₂O (one molecule decomposes)
- Bimolecular: 2HI → H₂ + I₂ (two molecules collide)
- Termolecular: 2NO + O₂ → 2NO₂ (three molecules collide simultaneously)
Reactions with molecularity greater than three are extremely rare because the probability of more than three molecules colliding simultaneously is very low.
Rate Determining Step
In complex reactions involving multiple steps, the overall rate is controlled by the slowest step, called the rate-determining step. It’s like a traffic bottleneck; no matter how fast other lanes move, the overall speed is limited by the slowest lane.
Example: Decomposition of H₂O₂ catalyzed by I⁻
Overall reaction: 2H₂O₂ → 2H₂O + O₂
Mechanism:
Step 1: H₂O₂ + I⁻ → H₂O + IO⁻ (slow)
Step 2: H₂O₂ + IO⁻ → H₂O + I⁻ + O₂ (fast)
The rate law is determined by step 1: Rate = k[H₂O₂][I⁻]
Pseudo First Order Reactions
Sometimes higher-order reactions behave as if they are first order due to experimental conditions.
Example: Hydrolysis of ethyl acetate
CH₃COOC₂H₅ + H₂O → CH₃COOH + C₂H₅OH
This is actually a second-order reaction, but when water is in large excess, its concentration doesn’t change during the reaction. The reaction then appears to be first order with respect to ethyl acetate only.
Rate = k’[CH₃COOC₂H₅] where k’ = k[H₂O]
Integrated Rate Equations
Through differential rate equations, we get the rate of reaction at any instant, and integrated rate equations connect concentrations at different times with the rate constant.
The integrated rate equation is different for different reaction orders. For example:
Zero Order Reactions
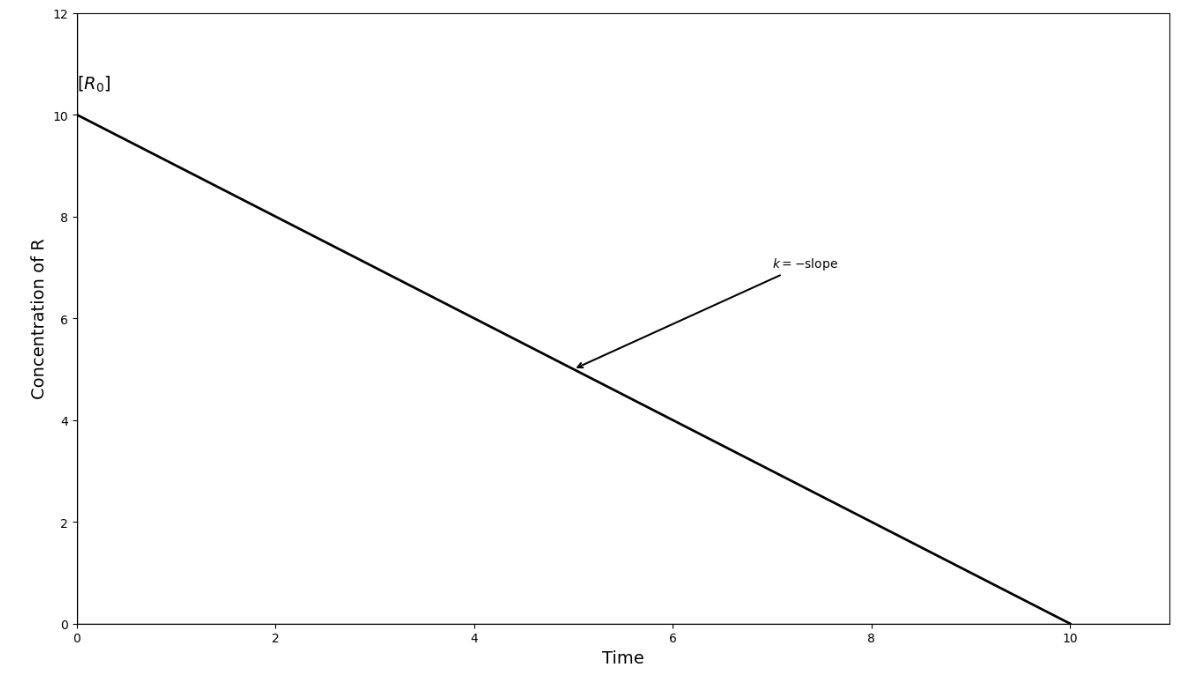
In zero-order reactions, the reaction rate remains constant throughout the whole process, regardless of reactant concentration. It happens under special conditions, like when a catalyst surface becomes saturated.
For the reaction R → P with zero-order kinetics:
Rate equation: Rate = k[R]⁰ = k
Integrated form: [R] = [R]₀ - kt
Where.
[R]₀ is the initial concentration at t = 0.
Examples:
- Decomposition of NH₃ on the platinum surface at high pressure
- Some enzyme-catalyzed reactions occur when the enzyme is saturated
First Order Reactions
First-order reactions are most common in chemistry. In first order reaction, the rate is directly proportional to the concentration of one reactant.
For the reaction R → P:
Rate equation: Rate = k[R]
Integrated forms:
- Exponential form: [R] = [R]₀e^(-kt)
- Logarithmic form: ln[R] = ln[R]₀ - kt
- Common log form: log([R]₀/[R]) = kt/2.303
Examples:
- Radioactive decay: ²²⁶Ra → ²²²Rn + ⁴He
- Decomposition of N₂O₅: 2N₂O₅ → 4NO₂ + O₂
- Many organic reactions in dilute solutions
First Order Gas Phase Reactions
Integrated rate law expressed as partial pressures for the gaseous reaction at the same temperatures.
For A(g) → B(g) + C(g):
If pᵢ = initial pressure of A and pₜ = total pressure at time t:
- Pressure of A at time t: pₐ = 2pᵢ - pₜ
- Integrated equation: k = (2.303/t) log(pᵢ/pₐ)
Half-Life of Reactions
The time required for the concentration of a reactant to come down to half its initial value is called the half-life. It’s useful for comparing reaction rates.
For zero order: t₁/₂ = [R]₀/2k
- Half-life decreases as the reaction proceeds
- Depends on initial concentration
For first order: t₁/₂ = 0.693/k = ln2/k
- Half-life remains constant throughout the reaction
- Independent of initial concentration
Temperature Dependence of the Rate of a Reaction
Most chemical reactions increase their rate or speed with even a small increase in temperature. A general thumb rule is that reaction rates approximately double for every 10°C increase in temperature.
The Arrhenius Equation
The relationship between reaction rate and temperature was quantitatively described by Svante Arrhenius. His equation connects the rate constant with temperature.
k = Ae^(-Eₐ/RT)
Where,
- k = rate constant
- A = Arrhenius factor (frequency factor)
- Eₐ = activation energy (J/mol)
- R = gas constant (8.314 J mol⁻¹ K⁻¹)
- T = absolute temperature (K)
Activation Energy
Activation energy is the minimum energy required for reactant molecules to form products.
- Higher Eₐ → slower reaction (few molecules have enough energy)
- Lower Eₐ → faster reaction (more molecules can overcome)
- Catalysts work by providing an alternative path with lower Eₐ
Maxwell-Boltzmann Distribution
The reason temperature affects the rate of reaction highly is because of how molecular energies are distributed.
- At any temperature, molecules have a range of kinetic energies
- Only molecules with energy ≥ Eₐ can react
- Higher temperature shifts the energy distribution to higher values
- Small temperature increases dramatically increase the fraction of molecules with energy ≥ Eₐ
The exponential term e^(-Eₐ/RT) in the Arrhenius equation represents the fraction of molecules with sufficient energy to react.
Effect of Catalyst
Catalysts a substances that increase reaction speed by providing an alternative reaction pathway with lower activation energy. Catalyst can affect the speed of reaction, but can’t change the occurring reaction.
How catalysts work:
- Provide an alternative mechanism with a smaller energy barrier
- Sometimes, increase the frequency of successful collisions
- Speed up forward and reverse reactions equally
- Doesn’t affect the final equilibrium position
There are three types of catalysis: Homogeneous, Heterogeneous, and Enzyme catalysis.
- Homogeneous: Catalyst in the same phase as the reactants
- Heterogeneous: Catalyst in a different phase (often a solid catalyst, liquid/gas reactants)
- Enzyme catalysis: Biological catalysts with extreme specificity and efficiency
Collision Theory of Chemical Reactions
Now, let’s understand the mechanical explanation of how a reaction takes place and why factors like temperature and concentration affect the speed of a reaction through collision theory.
The Collison theory is developed on the following assumptions:
- Chemical reactions happen when molecules of reactant collide with each other.
- Not all collisions make a reaction. Only collisions with energy higher than or equal to the activation energy (Eₐ) can result in a chemical reaction.
- Even high-energy collisions won’t result in a reaction until the molecules are oriented correctly.
For a bimolecular reaction A + B → Products:
Rate = Z_AB × P × e^(-Eₐ/RT)
Where:
- Z_AB = collision frequency between A and B molecules
- P = steric factor (probability of proper orientation)
- e^(-Eₐ/RT) = fraction of collisions with sufficient energy
Collision Frequency
The collision frequency depends on Concentration, Temperature, Molecular size, and Relative velocity.
Steric Factor
The steric factor or Probability Factor (P) accounts for the geometric requirements of the reaction. Not all collisions, even high-energy ones, lead to a reaction.
Factors affecting P:
- Molecular complexity, simple atoms/molecules have P ≈ 1, complex molecules have P << 1
- Some reactions require very specific orientations
- The arrangement of atoms during a collision affects success
Effective Collisions
For a collision to be effective, which results in a chemical reaction, two conditions must be met:
First is Threshold Energy, the total kinetic energy of colliding molecules must surpass the activation energy.
Threshold Energy = Activation Energy + Average kinetic energy of reactants
And second, proper orientation.
- Breaking bonds is weakened during a collision
- New bonds can form efficiently
- The reaction pathway is energetically favorable
Temperature Dependence Explained
Collision theory explains why temperature has such a strong effect on reaction rates. Higher temperature results in more collisions, more energetic collisions, higher average energy of reactants, and a greater fraction of molecules with E ≥ Eₐ.
Limitations of Collision Theory
Here are some limitations of collision theory.
- Treats molecules as hard spheres, ignoring their internal structure and flexibility.
- Works best for gas-phase reactions between small molecules.
- Doesn’t fully address reactions involving intermediates or multiple steps.
- Doesn’t explain how solvents affect reaction rates in solution.
Chemical Kinetics Formulas
You can check all the important formulas of chemical kinetics in the table below:
| Concept | Formula |
|---|---|
| Rate of reaction | |
| Rate law expression | |
| Integrated rate law (1st order) | |
| Half-life (1st order) | |
| Integrated rate law (2nd order) | |
| Half-life (2nd order) | |
| Arrhenius equation | |
| Slope form of Arrhenius equation | |
| Relation between rate constants |
Read more: Chemical Kinetics NCERT PDF
Revision Notes for Class 12 Chemistry
NCERT Solutions for Class 12 Chemistry
Chemical Kinetics FAQs
Commonly asked questions
What is reaction kinetics?
Reaction Kinetics, also known as chemical kinetics, is the study of the rate of chemical reaction and the factors affecting the reaction rate, such as temperature, concentration, and catalyst.
Can the order and molecularity of a reaction be the same?
Yes, in elementary reactions, order and molecularity can be the same, but this is not always the case because order is an experimental quantity, and molecularity is a theoretical concept.
What is the difference between reaction rate and rate constant?
Reaction rate is used to measure how fast or slow reactions occur per unit time. The rate constant is a proportionality factor that remains constant for every reaction.
Chemistry Chemical Kinetics Exam