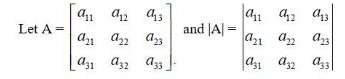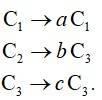Class 12th
Get insights from 12k questions on Class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
8 months agoContributor-Level 10
Option 'C' is correct as determinant is a number associated to a square matrix.
New answer posted
8 months agoContributor-Level 10
This is a Long Answer Type Questions as classified in NCERT Exemplar
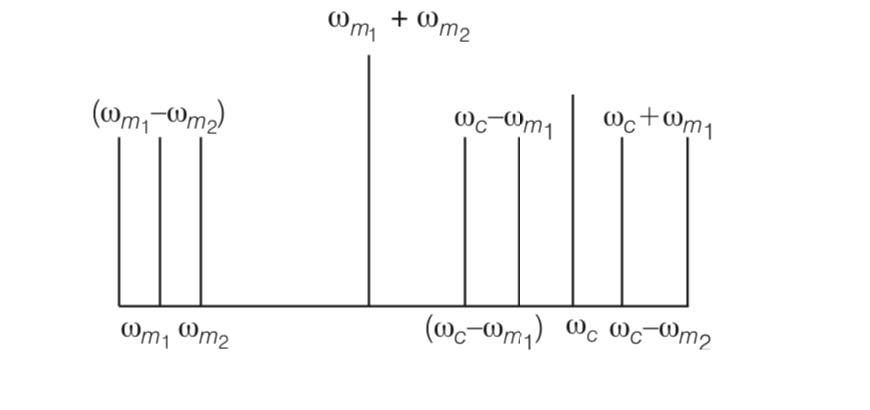
in first case crowding spectrum is visible
If we want more wave to be modulated then more crowding will occur and more mixing up of signal.
But we want to accommodate this we use higher band width and frequency career wave
New answer posted
8 months agoContributor-Level 10
This is a Long Answer Type Questions as classified in NCERT Exemplar
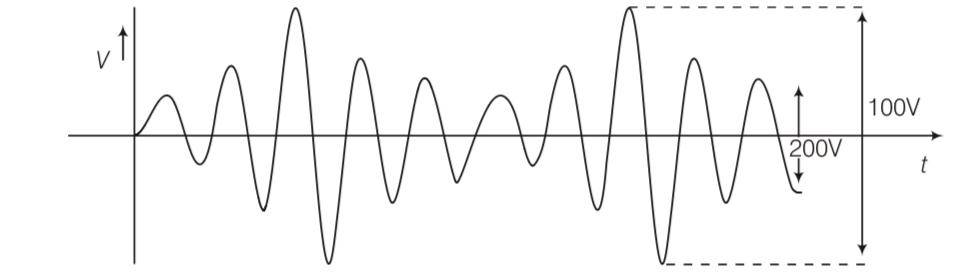
Maximum voltage = 100/2 = 50V
And minimum voltage = 20/2 = 10V
Percentage modulation= max voltage -min voltage/ max voltage + min voltage
= = 66.67%
Peak career voltage= max voltage+ min voltage/2= 50+10/2=30V
Peak value of information voltage= 66.67/100 30= 20V
New answer posted
8 months agoContributor-Level 10
This is a Long Answer Type Questions as classified in NCERT Exemplar
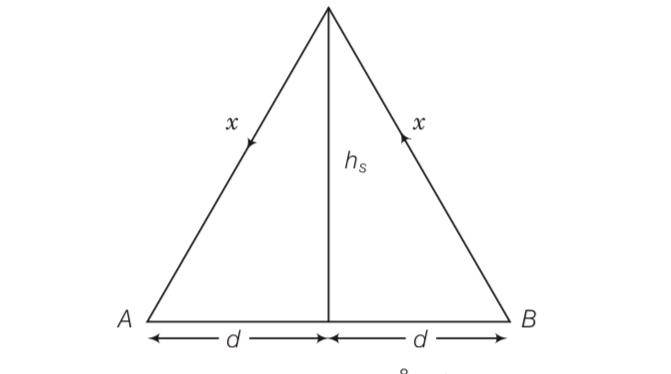
height of satellite hs= 600km
As we know velocity = distance/time
2x/4.0410-3 = 38
So x=606 km after solving
According to Pythagoras theorem d2=x2-h2= 6062-6002= 7236
So d= 85.06km so total distance will be double from receiver to transmitter = 170.1km
And d = √2Rh
h=7236/2*6400 = 565m
New answer posted
8 months agoContributor-Level 10
This is a Long Answer Type Questions as classified in NCERT Exemplar
as we know that I= I0
And I= 25%of I0=
I=I0/4
I0/4= I0
I0 cancel from both sides
¼=
Taking log on both sides log1 -log4= - loge
X= log4/
New answer posted
8 months agoContributor-Level 10
LHS =
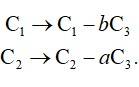

= (1 + a2 + b2)2 [(1 -a2 + b2) - 2a (-a)]
= (1 + a2 + b2)2 (1 -a2 + b2 + 2a2)
= (1 + a2 + b2)2 (1 + a2 + b2)
= (1 + a2 + b2)3 = R.H.S.
New answer posted
8 months agoContributor-Level 10
LHS =
R1→ R1 + R2 + R3
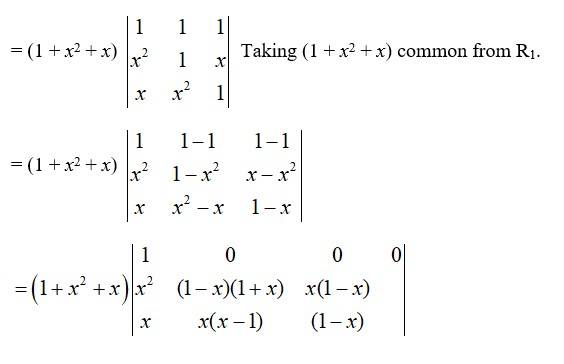
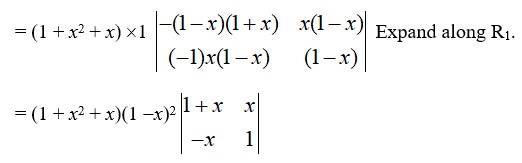
= (1 + x2 + x) (1 -x)2 [ (1 + x)* 1 - (-x) x].
= (1 + x2 + x) (1 -x)2 (1 + x + x2).
= { (1 + x2 + x) (1 -x)}2
= {1 -x + x2-x3 + x-x2}2
= (1 -x3)2 = R.H.S.
New answer posted
8 months agoContributor-Level 10
(i) LHS =
R1→ R1 + R2 + R3
= (a + b + c) Taking (a + b + c) common from R1
= (a + b+ c)
= (a + b + c)
= (a + b + c) * 1. Expand along R1
= (a + b + c){(a + b + c)2- 0}
= (a + b +c)3 = R.H.S
(ii) LHS =
C1→ C1 + C2 + C3.
= 2 (k + y + z) Taking 2
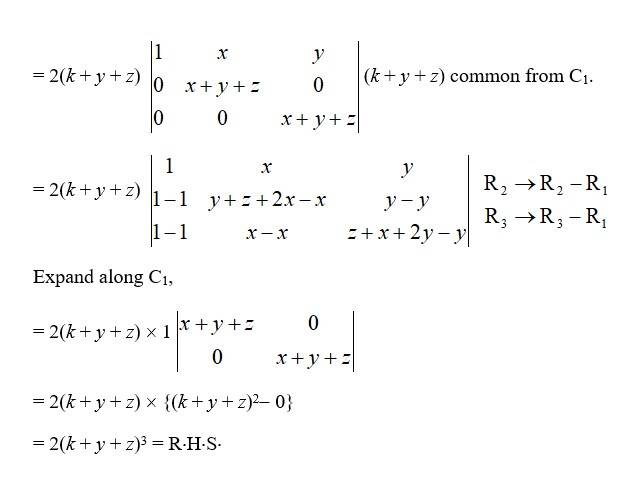
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 684k Reviews
- 1800k Answers