Conic Sections
Get insights from 199 questions on Conic Sections, answered by students, alumni, and experts. You may also ask and answer any question you like about Conic Sections
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
4 weeks agoContributor-Level 9
Equation of chord of x² + y² = 25 with mid point (h, k) is xh + yk = h² + k².
Or, y = (-h/k)x + (h² + k²)/k.
If this touches the ellipse x²/9 + y²/16 = 1, then the condition for tangency c² = a²m² + b² must be satisfied.
Here, m = -h/k, c = (h²+k²)/k, a²=9, b²=16.
(h² + k²)/k)² = 9 (-h/k)² + 16
(h² + k²)²/k² = 9h²/k² + 16
⇒ (h² + k²)² = 9h² + 16k²
∴ Required locus (x² + y²)² = 9x² + 16y².
New answer posted
4 weeks agoContributor-Level 9
y² - 2x = 4√ (y² - 2x + 1)
Let y² - 2x = k.
k = 4√ (k+1) ⇒ k² = 16 (k+1) ⇒ k²-16k-16=0
(This appears to be from another problem. The provided solution text says:)
y² = 2x = 4 (1/2 x)
a > 2 * (1/2) ⇒ a > 1.
New answer posted
4 weeks agoContributor-Level 10
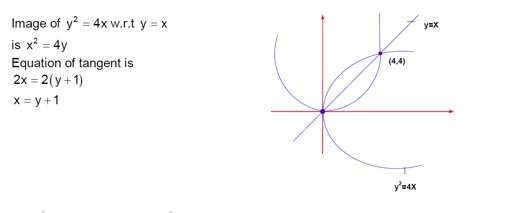
The tangent to the parabola y² = 4ax is y = mx + a/m.
For y² = 4x, a=1. So, the tangent is y = mx + 1/m.
The given line is y = mx + 4.
Comparing the two, 1/m = 4 ⇒ m = 1/4.
The line is y = (1/4)x + 4.
This line is also tangent to x² = 2by.
Substitute y into the parabola equation:
x² = 2b (1/4)x + 4)
x² = ( b/2 )x + 8b
x² - ( b/2 )x - 8b = 0.
For tangency, the discriminant (D) is zero.
D = (-b/2)² - 4 (1) (-8b) = 0.
b²/4 + 32b = 0.
b ( b/4 + 32) = 0.
b = 0 (not possible) or b/4 = -32 ⇒ b = -128.
New answer posted
4 weeks agoContributor-Level 10
Given 2ae = 6 and 2a/e = 12.
From these, ae = 3 and a/e = 6.
Multiplying the two equations: (ae) (a/e) = 3 * 6 => a² = 18.
We know that b² = a² (1 - e²) = a² - a²e² = 18 - (ae)² = 18 - 3² = 18 - 9 = 9.
The length of the latus rectum (L.R.) is 2b²/a.
L.R. = 2 * 9 / √18 = 18 / (3√2) = 6/√2 = 3√2.
New answer posted
4 weeks agoContributor-Level 10
The point of intersection of the ellipse x²/16 + y²/b² = 1 and the curve y² = 3x² lies on both.
Substitute y² = 3x² into the ellipse equation:
x²/16 + 3x²/b² = 1
x² (1/16 + 3/b²) = 1
x² (b² + 48) / 16b² = 1
x² = 16b² / (b² + 48).
For a solution to exist, we need x² > 0, which is true if b≠0.
The problem seems to have a condition missing or misinterpreted in the OCR. The provided solution also shows x² + y² = 4b, which might be another curve involved. Assuming the point lies on x²+y²=4b.
x² + 3x² = 4b => 4x² = 4b => x² = b.
Substitute x²=b into the ellipse equation: b/16 + 3b/b² = 1 (assuming y²=3b).
b/16 + 3/b = 1
New question posted
a month agoNew answer posted
a month agoContributor-Level 10
The equation of the tangent to the ellipse x²/27 + y² = 1 at the point (3√3 cosθ, sinθ) is:
x (3√3 cosθ)/27 + y (sinθ)/1 = 1 ⇒ x/ (3√3) cosθ + y sinθ = 1.
To find the intercepts on the axes:
x-intercept (set y=0): x = 3√3 / cosθ = 3√3 secθ.
y-intercept (set x=0): y = 1 / sinθ = cosecθ.
The sum of the intercepts is z (θ) = 3√3 secθ + cosecθ.
To find the minimum value of z, we differentiate with respect to θ and set it to zero:
dz/dθ = 3√3 secθ tanθ - cosecθ cotθ = 0.
3√3 (sinθ/cos²θ) = cosθ/sin²θ.
3√3 sin³θ = cos³θ ⇒ tan³θ = 1/ (3√3).
⇒ tanθ = 1/√3.
Since θ ∈ (0, π/2), the solution
New answer posted
a month agoContributor-Level 10
The equation is for a hyperbola: x²/4 - y²/2 = 1.
The eccentricity e is given by e = √ (1 + b²/a²) = √ (1 + 2/4) = √6/2.
The focus F is at (ae, 0), which is (2 * √6/2, 0) = (√6, 0).
The equation of the tangent at a point P (x? , y? ) is xx? /a² - yy? /b² = 1.
The equation of the tangent at P is given as x - (√6 y)/2 = 1.
This tangent cuts the x-axis (y=0) at x=1, so Q is (1, 0).
The latus rectum is the line x = ae = √6.
To find the point R where the tangent intersects the latus rectum, we substitute x=√6 into the tangent equation:
√6 - (√6 y)/2 = 1 ⇒ √6 - 1 = (√6 y)/2 ⇒ y = 2 (√6 - 1)/√6.
The vertices o
New answer posted
a month agoContributor-Level 10
Given a triangle with inradius r and circumradius R.
The inradius r is calculated as r = |0 + 0 - 3| / √2 = 3 / √2.
From the geometry of the triangle, we have the relation r/R = sin (30°) = 1/2.
This gives R = 2r.
The question asks for the sum R + r, which is 2r + r = 3r.
Substituting the value of r, we get 3 * (3/√2) = 9/√2.
∴ R + r = 9/√2.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 688k Reviews
- 1800k Answers