Maths

Let the number of chocolates given to C₁, C₂, C₃ & C₄ be a, b, c, d respectively.

Given 4   $\le b\le 7$

$2\le c\le 6$

Now using these the maximum number of chocolates that can be given to C₁ or C₄ is 24 (where b & c are given 2 & 4 chocolates).

$\therefore 0\le a\le 24$

$0\le d\le 24$

& a + b + c + d = 30

So, total possible solution to the above equation.

Coefficient of x³⁰ in.

$\left(x^0+x+x^2+....+x^{24}\right)\left(x^4+x^5+....+x^7\right)\left(x^2+x^3+....+x^6\right)\left(x^0+x+x^2+....+x^{24}\right)$

=  ${\left(1+....+x^{24}\right)}^2\left(x^4\right)\left(1+x+....+x^3\right)*x^2\left(1+x+....+x^4\right)$

$=\left(x^{56}-2x^{31}+x^6\right)*\left(x^9-x^4-x^5+1\right)*{\left(x-1\right)}^{-4}$

x⁵⁶ & x³¹ can never give x³⁰ so we discard them.

$x^6*x^9*{\left(x-1\right)}^{-4}{\to }^{15+4-1}\text{?}{C}_{4-1}{=}^{18}\text{?}{C}_3$

Coefficient x³⁰ ® ¹⁸C₃ – ²³C₃ – ²²C₃ + ²⁷C₃

=   $\frac{18*17*16}{6}-\frac{23*22*21}{6}-\frac{22*21*20}{6}+\frac{27*26*25}{6}$

= 430

$f\left(-2\right)+f\left(3\right)=0.$ One root of f (x) = 0 is (-1)

Let's assume other root to be a

$\therefore f\left(x\right)=a\left(x+1\right)\left(x-\alpha \right)$

Given that f (-2) + f (3) = 0

a (-2 + 1) (-2 -a) + a (3 + 1) (3 - a) = 0

Þ 14 -3a = 0 Þ a =    $\frac{14}{3}$

$\therefore$ sum of roots =   $\frac{14}{3}-1=\frac{11}{3}$

R₁ =  $\left\{\left(a,1\right)\in N*N:\left|a-b\right|\le 13\right\}$

 $\left(a,a\right)\in R_{1}as\left|a-a\right|\le 13\left(Reflexive\right)$

$\left(a,b\right)\&\left(b,a\right)\in R_{1}as\left|a-b\right|=\left|b-a\right|\to \left(symmetric\right).$

But it is not necessary that if (a,b) & (b, c)  $\in R,then\left(a,c\right)\in R$

Eg   $-\left(21,10\right)\in R\&\left(10,1\right)\in Rbut\left(21,1\right)\notin R_1$

R₂ =   $\left\{\left(a,b\right)\in N*N:\left|a-b\right|\ne 13\therefore R_2\to Notequivalencesolutoin.\right\}$

$\left(a,b\right)\&\left(b,a\right)\in R_{2}as\left|a-b\right|=\left|b-a\right|$

But it is not necessary that if (a, b) & (b, c)  $\in R_2$  then (a, c) also $\in R_2$ .

Eg – (21, 1)   $\in R_2\&\left(1,8\right)\in R_{2}but\left(21,8\right)\notin R_2$

$f\left(x\right)=a{x}^2+bx+c$  

g (x) = px + q

$f\left(g\left(x\right)\right)=a{\left(px+q\right)}^2+b\left(p\right)\left(+q\right)+c$                

$\Rightarrow 8x^2-2x=a{\left(px+q\right)}^2+b\left(px+q\right)+c$                

Compare 8 = ap² …………… (i)

-2 = a (2pq) + bp

0 = aq² + bq + c

$9\left(f\left(x\right)\right)=p\left(a{x}^2+bx+c\right)+q$                

? 4x² + 6x + 1 = apx² + bpx + cp + q

? Andhra Pradesh = 4 ……………. (ii)

6 = bp

1 = cp + q

From (i) & (ii), p = 2, q = -1

? b = 3, c = 1, a = 2

f (x) = 2x² + 3x + 1

f (2) = 8 + 6 + 1 = 15

g (x) = 2x – 1

g (2) = 3

$N=M^2+M^4+.....+M^{98}$

$=\left(-{\alpha }^{2}I\right)+{\left(-{\alpha }^{2}I\right)}^2+....+{\left(-{\alpha }^{2}I\right)}^{49}$

$=I\left(-{\alpha }^2+{\alpha }^4-{\alpha }^6+....-{\alpha }^{98}\right)$

N = $-I\left({\alpha }^2-{\alpha }^4+{\alpha }^6.......+{\alpha }^{98}\right)$

$=-I\frac{{\alpha }^2\left(1-{\left(-{\alpha }^2\right)}^{49}\right)}{1-\left(-{\alpha }^2\right)}$

N = $\frac{-I{\alpha }^2\left(1+{\alpha }^{98}\right)}{1+{\alpha }^2}$

Now $\left(I-m^2\right)N=-2I$

$\left(I+{\alpha }^{2}I\right)\frac{\left(-I{\alpha }^2\cdot (1+{\alpha }^{98}\right)}{1+{\alpha }^2}=-2I$

? α¹⁰⁰ + α² = 2

? α = $\pm 1$

Fix the unit place, find the chances for the first three digits

unit digit as 1, total ways = 9.10²

unit digit as 2, total ways = 4.5²

unit digit as 3 total ways = 3.4²

unit digit as 4 total ways = 2.3²

unit digit as 5 total ways = 1.2²

unit digit as 6 total ways = 1.2²

unit digit as 7 total ways = 1.2²

unit digit as 8 total ways = 1.2²

unit digit as 9 total ways = 1.2²

$T_{r+1}{=}^{15}\text{?}{C}_r\cdot {\left(2x^{1/5}\right)}^{15-r}{\left(-x^{-1/5}\right)}^r$  

= ¹⁵C_r $\cdot 2^{15-r}\cdot x^{\frac{15-2r}{5}}\cdot {\left(-1\right)}^r$  

Coefficient of x^-1 ⇒ r = 10 ⇒ m = ¹⁵C₁₀ $\cdot 2^5$  

$x^{-3}\Rightarrow r=15\Rightarrow n{=}^{15}\text{?}{C}_{15}\cdot 2^0=1$               

now mn² = ¹⁵C_r   $\cdot 2^r$

⇒ r = 5

f (x) is an even function

$f\left(-\frac{1}{4}\right)=f\left(-\frac{1}{2}\right)=f\left(\frac{1}{2}\right)=f\left(\frac{1}{4}\right)=0$

So, f (x) has at least four roots in (-2, 2)

$g\left(\frac{-3}{4}\right)=g\left(\frac{3}{4}\right)=0$

So, g (x) has at least two roots in (2, 2)

now number of roots of f (x) $\cdot g"\left(x\right)=f\text{'}\left(x\right)\cdot g\text{'}\left(x\right)=0$

It is same as number of roots of $\frac{d}{dx}\left(f\left(x\right)\cdot g\text{'}\left(x\right)\right)=0$ will have atleast 4 roots in (2, 2)

Given a > b

Area common to x2 + y2 $\le a^{2}and\frac{x^2}{a^2}+\frac{y^2}{b^2}\le 1$

is $\pi a^2-\pi ab=30\pi ..............\left(i\right)$

Similarly $\pi ab-\pi b^2=18\pi .................\left(ii\right)$

Equation (i) and equation (ii) $\frac{a}{b}=\frac{5}{3}$

Equation (i) + equation (ii) $a^2-b^2=48$

a² = 75, b² = 27

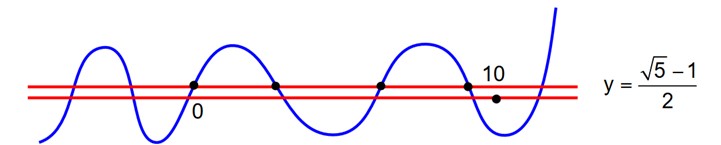
sin x = 1 – sin² x

sin x = $\frac{-1+\sqrt[]{5}}{2},\frac{-1-\sqrt[]{5}}{2}\left(rejected\right)$

draw y = sin x

y = $\frac{\sqrt[]{5}-1}{2},$ find their pt. of intersection.