Maths

 $\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-1}{2}=\frac{-2\left(1+4+2-16\right)}{1+2^2+2^2}$

(x, y, z) = (3, 6, 5)

now point Q and line both lies in the plane.

So, equation of plane is

$\left|\begin{array}{ccc}\hfill x\hfill & \hfill y\hfill & \hfill z+1\hfill \\ \hfill 3\hfill & \hfill 6\hfill & \hfill 6\hfill \\ \hfill 1\hfill & \hfill 2\hfill \end{array}\right|=0$

2x – z = 1

option (B) satisfies.

Let AB $\equiv x-2y+1=0$

AC $\equiv 2x-y+1=0$

So vertex A = (1, 1)

altitude from B is perpendicular to AC and passing through orthocentre.

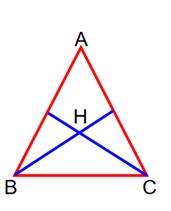
So, BH = x + 2y – 7 = 0

CH = 2x + y – 7 = 0

now solve AB & BH to get B (3, 2) similarly CH and AC to get C (2, 3) so centroid is at (2, 2)

Line $\perp$ to the normal

⇒ 3p + 2q – 1 = 0

$\left(2,-1,-3\right)$ lies in the plane 2p + q = 8

From here p = 15, q = -22

Equation of plane 15x – 22y + z – 5 = 0

Distance from origin = $\left|\frac{5}{\sqrt[]{15^2+{\left(-22\right)}^2+1^2}}\right|$$=$√5/142

${\left(x-\frac{1}{\sqrt[]{2}}\right)}^2+{\left(y-\frac{1}{\sqrt[]{2}}\right)}^2=1$

here AB = $\sqrt[]{2}$ , BC = 2, AC = $\sqrt[]{2}$

area = $\frac{1}{2}*\sqrt[]{2}*\sqrt[]{2}=1$

Tangents making angle $\frac{\pi }{4}$ with y = 3x + 5.

$tan\frac{\pi }{4}=\left|\frac{m-3}{1+3m}\right|\Rightarrow m=-2,\frac{1}{2}$

So, these tangents are $\perp$ . So ASB is a focal chord.

$\Rightarrow {\displaystyle \underset{}{\overset{}{\int }}\frac{dy}{1+y^2}=-2{\displaystyle \underset{}{\overset{}{\int }}\frac{e^{x}dx}{1+{\left(e^x\right)}^2}+C}}$

$\Rightarrow ta{n}^{-1}y=-2\cdot ta{n}^{-1}{e}^x+C$

x = 0, y = 0

$\Rightarrow 0=2ta{n}^{-1}+C$

$C=+\frac{\pi }{2}$

now at x = $\mathcal{l}n\sqrt[]{3}$

$ta{n}^{-1}y=-2ta{n}^{-1}\left(e^{\mathcal{l}n\sqrt[]{3}}\right)+\frac{\pi }{2}$

$6\left(y\text{'}\left(0\right)+{\left(y\left(\mathcal{l}n\sqrt[]{3}\right)\right)}^2\right)=6\left(-1+\frac{1}{3}\right)=-4$

 ${\displaystyle \underset{0}{\overset{2}{\int }}\sqrt[]{2xdx}}-{\displaystyle \underset{0}{\overset{2}{\int }}\sqrt[]{2x-x^{2}dx}}={\displaystyle \underset{0}{\overset{1}{\int }}dy}-{\displaystyle \underset{0}{\overset{1}{\int }}\sqrt[]{1-y^2}dy-{\displaystyle \underset{0}{\overset{2}{\int }}\frac{y^2}{2}dy}+{\displaystyle \underset{1}{\overset{2}{\int }}2dy+I}}$

$\Rightarrow \frac{8}{3}-{\displaystyle \underset{0}{\overset{1}{\int }}\sqrt[]{1-t^2}dt}=1-\frac{8}{6}+2+I$

$I=1-{\displaystyle \underset{0}{\overset{1}{\int }}\sqrt[]{1-t^2}dt}$

$f\left(x\right)=x+x{\displaystyle \underset{0}{\overset{1}{\int }}f\left(t\right)dt}-{\displaystyle \underset{0}{\overset{1}{\int }}{t}_{0}f\left(t\right)dt}$

Let $1+{\displaystyle \underset{0}{\overset{1}{\int }}f}\left(t\right)dt=\alpha$

${\displaystyle \underset{0}{\overset{1}{\int }}tf\left(t\right)dt=\beta }$

So, f (x) = αx – β

Now, $\alpha ={\displaystyle \underset{0}{\overset{1}{\int }}f\left(t\right)dt+1}$

$\alpha ={\displaystyle \underset{0}{\overset{1}{\int }}\left(at-\beta \right)dt+1}$

$\beta ={\displaystyle \underset{0}{\overset{1}{\int }}t\cdot f\left(t\right)dt}$

$\beta =\frac{4}{13},\alpha =\frac{18}{13}$

f (x) = αx – β

$=\frac{18x-4}{13}$

option (D) satisfies

$f\text{'}\left(x\right)=\frac{n_1\cdot f\left(x\right)}{x-3}+n_2\cdot \frac{f\left(x\right)}{x-5}$

$=\frac{f\left(x\right)\cdot \left(n_1+n_2\right)}{\left(x-3\right)\left(x-5\right)}\left(x-\frac{\left(5n_1+3n_2\right)}{n_1+n_2}\right)$

$f\text{'}\left(x\right)={\left(x-3\right)}^{n_1-1}\cdot {\left(x-5\right)}^{n_2-1}\cdot \left(n_1+n_2\right)\left(x-\frac{\left(5n_1+3n_2\right)}{n_1+n_{2l}}\right)$

option (C) is incorrect, there will be minima.

 $x^4-2x^3+2x-1={\left(x-1\right)}^2\left(x^2-1\right)$

$sin\pi x=sin(\pi \left(1-x\right)$

$=-sin\left(sin\pi \left(x-1\right)\right)$

$\underset{x\to 1}{lim}\frac{\left(x^2-1\right)\cdot si{n}^2\pi x}{\left(x^2-1\right){\left(x-1\right)}^2}=\underset{x\to 1}{lim}\frac{si{n}^2\left(\pi \left(x-1\right)\right)}{{\left(x-1\right)}^2}$

$=\underset{x\to 1}{lim}\frac{si{n}^2\left(\pi \left(x-1\right)\right)}{{\left(\pi \left(x-1\right)\right)}^2}\cdot {\pi }^2$

= 2