Maths

 $\frac{dy}{dx}=\frac{1}{1+sin2x}$

$dy=\frac{se{c}^{2}xdx}{{\left(1+tanx\right)}^2}$

$\Rightarrow y=-\frac{1}{1+tanx}+c$

When

$x=\frac{\pi }{4},y=\frac{1}{2}$ gives c = 1

So

$x+\frac{\pi }{4}=\frac{5\pi }{6}or\frac{13\pi }{6}\Rightarrow x=\frac{7\pi }{12}or\frac{23\pi }{12}$

sum of all solutions =

$\pi +\frac{7\pi }{12}+\frac{23\pi }{12}=\frac{42\pi }{12}$

Hence k = 42

Each element of ordered pair (i, j) is either present in A or in B.

So, A + B = Sum of all elements of all ordered pairs {i, j} for $1\le i\le 10$ and $1\le j\le 10$

= 20 (1 + 2 + 3 + … + 10) = 1100

$l=\frac{48}{{\pi }^4}{\displaystyle {\int }_0^{\pi }\left[{\left(\frac{\pi }{2}-x\right)}^3-\frac{3{\pi }^2}{4}\left(\frac{\pi }{2}-x\right)+\frac{{\pi }^3}{4}\right]\frac{sinxdx}{1+co{s}^{2}x}}$

Using

${\displaystyle {\int }_a^{b}f\left(x\right)dx={\displaystyle {\int }_a^{b}f\left(a+b-x\right)dx}}$

we get

$l=\frac{48}{{\pi }^4}{\displaystyle {\int }_0^{\pi }\left[-{\left(\frac{\pi }{2}-x\right)}^3+\frac{3{\pi }^2}{4}\left(\frac{\pi }{2}-x\right)+\frac{{\pi }^3}{4}\right]\frac{sinxdx}{1+co{s}^{2}x}}$

Adding these two equations, we get

$\Rightarrow l=\frac{12}{\pi }{\left[-ta{n}^{-1}\left(cosx\right)\right]}_0^{\pi }=\frac{12}{\pi }.\frac{\pi }{2}=6$

Sum of all elements of $A\cap B=2$  [Sum of natural number upto 100 which are neither divisible by 3 nor by 5]

$=2\left[\frac{100*101}{2}-3\left(\frac{33*34}{2}\right)-5\left(\frac{20*21}{2}\right)+15\left(\frac{6*7}{2}\right)\right]$

= 10100 – 3366 – 2100 + 630

= 5264

$\left(sin10°.sin50°.sin70°\right).\left(sin10°.sin20°.sin40°\right)$

$=\left(\frac{1}{4}sin30°\right).\left[\frac{1}{2}sin10°\left(cos20°-cos60°\right)\right]$

$=\frac{1}{32}\left[sin30°-sin10°-sin10°\right]$

$\frac{1}{64}-\frac{1}{16}sin10°$

Clearly $\alpha =\frac{1}{64}$

Hence 16 + a^-1 = 80

 $\left(4+x^2\right)dy-2x\left(x^2+3y+4\right)dx=0$

$\Rightarrow \frac{dy}{dx}=\left(\frac{6x}{x^2+4}\right)y+2x$

$e^{-3\mathcal{l}n\left(x^2+4\right)}=\frac{1}{{\left(x^2+4\right)}^3}$

So

$\frac{y}{{\left(x^2+4\right)}^3}={\displaystyle \int \frac{2x}{{\left(x^2+4\right)}^3}dx+c}$

$\Rightarrow y=-\frac{1}{2}\left(x^2+4\right)+c{\left(x^2+4\right)}^3$

When x = 0, y = 0 gives

$c=\frac{1}{32}$

So, for x = 2, y = 12

$\therefore {\displaystyle \underset{-6}{\overset{0}{\int }}f\left(x\right)dx=2*\frac{1}{2}\left(2+5\right)*3=21}$

Let y = mx + c is the common tangent

$soc=\frac{1}{m}=\pm \frac{3}{2}\sqrt[]{1+m^2}\Rightarrow m^2=\frac{1}{3}$

so equation of common tangents will be

$y=\pm \frac{1}{\sqrt[]{3}}x\pm \sqrt[]{3}$

which intersects at Q (3, 0)

Major axis and minor axis of ellipse are 12 and 6. So eccentricity

$e^2=1-\frac{1}{4}=\frac{3}{4}$

and length of latus rectum

$=\frac{2b^2}{a}=3$

Hence

$\frac{\mathcal{l}}{e^2}=\frac{3}{3/4}=4$

Boys (10)            Girls (5)

(3)                        (3)

B₁ & B₂ should not be selected together

Total number of ways

           

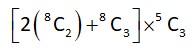
= (56 + 56) * 10 = 1120

$x^4?3x^3?2x^2+3x+1=0$

$?x=\pm 1$

and let, are roots of x2 – 3x – 1 = 0

$??+?=3??=?1$

$?1^3+{\left(?1\right)}^3+{?}^3+{?}^3$

= 27 + 3 (3) = 36