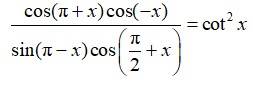Maths

The equation of any plane through the intersection of the planes,

$3x - y +2z ­-4=0and x + y + z -2=0,$ is

$\left(3x - y +2z -4\right)+\alpha \left(x + y + z -2\right)=0,where,\alpha \in R..........(1)$

The plane passes through the point $\left(2,2,1\right).$ Therefore, this point will satisfy equation (1).

$\begin{array}{l}\therefore (3*2-2+2*1-4)+\alpha (2+2+1-2)=0\\ \Rightarrow 2+3\alpha =0\\ \Rightarrow \alpha =-\frac{2}{3}\end{array}$

Substituting $\alpha =-\frac{2}{3}$ in equation (1), we obtain

$\begin{array}{l}(3x-y+2z-4)-\frac{2}{3}(x+y+z-2)=0\\ \Rightarrow 3(3x-y+2z-4)-2(x+y+z-2)=0\\ \Rightarrow (9x-3y+6z-12)-2(x+y+z-2)=0\\ \Rightarrow 7x-5y+4z-8=0\end{array}$

The equation of the plane ZOX is

y = 0

Any plane parallel to it is of the form,  y = a

Since the y-intercept of the plane is 3,

∴ a = 3

Thus, the equation of the required plane is y = 3

$2x+y-z=5 .........\left(1\right)$

Dividing both sides of equation (1) by 5, we obtain

$\begin{array}{l}\frac{2}{5}x+\frac{y}{5}-\frac{z}{5}=1\\ \Rightarrow \frac{x}{\frac{5}{2}}+\frac{y}{5}+\frac{z}{-5}=1..........(2)\end{array}$

It is known that the equation of a plane in intercept form is $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$ , where a,  b,  c are the intercepts cut off by the plane at x,  y, and z axes respectively.

Therefore, for the given equation,

$a=\frac{5}{2},b=5andc=-5$

Thus, the intercepts cut off by the plane are $\frac{5}{2}$ $,5and-5.$

23. (i) sin 75°= sin (45°+30°)

Using sin (x + y)= sin x cos y + cos x sin y we can write

41. Kindly consider the following

We know that through three collinear points $A,B,C$ i.e., through a straight line, we can pass an infinite number of planes.

(a) The given points are $A\left(1,1,-1\right),B\left(6,4,-5\right),andC\left(-4,-2,3\right).$

$\begin{array}{l}\left|\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill -1\hfill \\ \hfill 6\hfill & \hfill 4\hfill & \hfill -5\hfill \\ \hfill -4\hfill & \hfill -2\hfill & \hfill 3\hfill \end{array}\right|=(12-10)-(18-20)-(-12+16)\\ \end{array}$

$\begin{array}{l}=2+2-4\\ =0\end{array}$

Since $A,B,C$ are collinear points, there will be infinite number of planes passing through the given points.

(b) The given points are $A\left(1,1,0\right),B\left(1,2,1\right),andC\left(-2,2,-1\right).$

$\left|\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 2\hfill & \hfill 1\hfill \\ \hfill -2\hfill & \hfill 2\hfill & \hfill -1\hfill \end{array}\right|=(-2-2)-(2+2)=-8\ne 0$

Therefore, a plane will pass through the points A, B, and C.

It is known that the equation of the plane through the points,  $(x_1, y_1, z_1),(x_2, y_2, z_2)\&(x_3, y_3, z_3)$ , is

$\begin{array}{l}\left|\begin{array}{ccc}\hfill x-x_1\hfill & \hfill y-y_1\hfill & \hfill z-z_1\hfill \\ \hfill x_2-x_1\hfill & \hfill y_2-y_1\hfill & \hfill z_2-z_1\hfill \\ \hfill x_3-x_1\hfill & \hfill y_3-y_1\hfill & \hfill z_3-z_1\hfill \end{array}\right|=0\\ \Rightarrow \left|\begin{array}{ccc}\hfill x-1\hfill & \hfill y-1\hfill & \hfill z\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill -3\hfill & \hfill 1\hfill & \hfill -1\hfill \end{array}\right|=0\\ \Rightarrow (-2)(x-1)-3(y-1)+3z=0\\ \Rightarrow -2x-3y+3z+2+3=0\\ \Rightarrow -2x-3y+3z=-5\\ \Rightarrow 2x+3y-3z=5\end{array}$

This is the Cartesian equation of the required plane.

40. Kindly go through the solution